分析:由不等式的性质与充要条件的定义进行推理,得①不正确;由积分计算公式和微积分基本定理,可得②的积分计算正确;根据a+b=2将1=
(a+b)代入y表达式,再利用基本不等式算出y的最小值为
,得③正确;根据指数运算性质算出a=2,再由诱导公式和特殊角的三角函数值,算出
tan的值为
-,得④正确;根据三角函数图象的对称中心的公式,算出函数
f(x)=2sin(2x-)-1图象的对称中心为
(+,1)(k∈Z),故⑤不正确.
解答:解:对于①,若“x<-1”成立,则“x<-2”不一定成立.
反之,若“x<-2”成立,则“x<-1”一定成立.
因此“x<-1”是“x<-2”的必要不充分条件,故①不正确;
对于②,由积分公式可得
(ex+sinx)dx=(e
x-cosx)
=(e
1-cos1)-(e
0-cos0)=e-cos1,故②正确;
对于③,由于a>0,b>0,a+b=2,
可得
y=+=
(a+b)(
+)=
(5+
+)≥
(5+2
)=
,
当且仅当b=2a=
时等号成立.
因此可得:
y=+的最小值为
,故③正确;
对于④,若点(a,9)在函数y=3
x的图象上,则9=3
a,可得a=2.
∴
tan=
tan=-
tan=-
,故④正确;
对于⑤,对函数
f(x)=2sin(2x-)-1,令
2x-=kπ(k∈Z),可得x=
+
kπ(k∈Z),
所以函数
f(x)=2sin(2x-)-1图象的对称中心为
(+,1)(k∈Z),故⑤不正确.
综上所述,正确的命题是②③④.
故答案为:②③④
点评:本题给出几个命题,求出其中的真命题.着重考查了三角函数的图象与性质、三角函数的诱导公式、积分计算公式与微积分基本定理、利用基本不等式求最值和充要条件的判断等知识,属于中档题.



 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案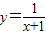 在(-∞,-1)∪(-1,+∞)上是减函数;
在(-∞,-1)∪(-1,+∞)上是减函数; ,则当x<0时,
,则当x<0时, ;
;