
分析 (1)设出B,C及BC中点坐标,利用点差法及重心坐标公式求出BC所在直线的斜率,则直线BC的方程可求;
(2)由A为90°,可得AB⊥AC,进一步得到x1x2+y1y2-14(y1+y2)+16=0,联立直线方程和椭圆方程,消元后由交轨法可得点D的轨迹方程.
解答 解:(1)由4x2+5y2=80,得$\frac{{x}^{2}}{20}+\frac{{y}^{2}}{16}=1$.
设B(x1,y1),C(x2,y2),BC中点为(x0,y0),BC所在直线的斜率为k,
则$\frac{{{x}_{1}}^{2}}{20}+\frac{{{y}_{1}}^{2}}{16}=1$,$\frac{{{x}_{2}}^{2}}{20}+\frac{{{y}_{2}}^{2}}{16}=1$.
两式作差得:$\frac{{{x}_{1}}^{2}-{{x}_{2}}^{2}}{20}+\frac{{{y}_{1}}^{2}-{{y}_{2}}^{2}}{16}=0$.
则$\frac{{x}_{0}}{5}+\frac{{y}_{0}k}{4}=0$.①
又由椭圆方程可得A(0,4),椭圆右焦点F(2,0),且已知F为三角形ABC的重心,
∴$\frac{{x}_{1}+{x}_{2}}{3}=2$,即x0=3.
$\frac{{y}_{1}+{y}_{2}+4}{3}=0$,即y0=-2.
把x0=3,y0=-2代入①,得$k=\frac{6}{5}$.
∴直线BC的方程为6x-5y-28=0;
(2)由AB⊥AC,得x1x2+y1y2-14(y1+y2)+16=0.②
设直线BC的方程为y=kx+b,
代入4x2+5y2=80,得(4+5k2)x2+10bkx+5b2-80=0.
${x}_{1}+{x}_{2}=\frac{-10bk}{4+5{k}^{2}},{x}_{1}{x}_{2}=\frac{5{b}^{2}-80}{4+5{k}^{2}}$,
则${y}_{1}+{y}_{2}=\frac{8k}{4+5{k}^{2}},{y}_{1}{y}_{2}$=$\frac{4{b}^{2}-80{k}^{2}}{4+5{k}^{2}}$.
代入②得:$\frac{9{b}^{2}-32b-16}{4+5{k}^{2}}=0$,解得:b=4(舍)或b=-$\frac{4}{9}$.
则直线过定点(0,-$\frac{4}{9}$),设D(x,y),
$\frac{y+\frac{4}{9}}{x}•\frac{y-4}{x}=-1$,整理得:9y2+9x2-32y-16=0.
∴点D的轨迹方程是${x}^{2}+(y-\frac{16}{9})^{2}=(\frac{20}{9})^{2}$(y≠4).
点评 本题考查椭圆的简单性质,考查了直线和圆锥曲线位置关系的应用,训练了利用“点差法”、“交轨法”求点的轨迹问题,属中档题.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:解答题
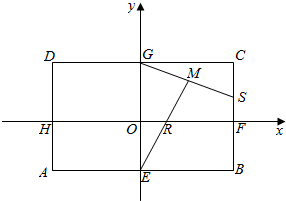 矩形ABCD中,|AB|=8,|BC|=6.E,F,G,H分别是矩形四条边的中点,R,S分别是线段OF和线段CF上的动点,且$\frac{OR}{OF}$=$\frac{CS}{CF}$=λ,建立如图所示的直角坐标系,O为矩形的对称中心,坐标轴分别平行于AB,BC.
矩形ABCD中,|AB|=8,|BC|=6.E,F,G,H分别是矩形四条边的中点,R,S分别是线段OF和线段CF上的动点,且$\frac{OR}{OF}$=$\frac{CS}{CF}$=λ,建立如图所示的直角坐标系,O为矩形的对称中心,坐标轴分别平行于AB,BC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 所有的质数都是奇数 | B. | ?x∈R,2x2+2≥2 | ||
| C. | 对每一个无理数x,x2也是无理数 | D. | 所有长度相等的向量均相等 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-e) | B. | (-e,-1) | C. | (1,e) | D. | (e,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com