
甲、乙两人破译一密码,它们能破译的概率分别为 和
和 ,试求:
,试求:
(1)两人都能破译的概率;
(2)两人都不能破译的概率;
(3)恰有一人能破译的概率;
(4)至多有一人能破译的概率;
(5)若要使破译的概率为99%,至少需要多少乙这样的人?
(1) (2)
(2) (3)
(3) (4)
(4) (5)16个
(5)16个
解析解:设事件A为“甲能译出”,事件B为“乙能译出”,则A、B相互独立,从而A与 、
、 与B、
与B、 与
与 均相互独立.
均相互独立.
(1)“两人都能译出”为事件AB,则
P(AB)=P(A)P(B)= ×
× =
= .
.
(2)“两人都不能译出”为事件
 ,则
,则
P(
 )=P(
)=P( )P(
)P( )=[1-P(A)][1-P(B)]
)=[1-P(A)][1-P(B)]
=
 =
= .
.
(3)“恰有一人能译出”为事件A +
+ B,又A
B,又A 与
与 B互斥,则P(A
B互斥,则P(A +
+ B)=P(A
B)=P(A )+P(
)+P( B)
B)
=P(A)P( )+P(
)+P( )P(B)
)P(B)
= ×
× +
+ ×
× =
= .
.
(4)“至多一人能译出”为事件A +
+ B+
B+
 ,且A
,且A 、
、 B、
B、
 互斥,故
互斥,故
P(A +
+ B+
B+
 )
)
=P(A)P( )+P(
)+P( )P(B)+P(
)P(B)+P( )P(
)P( )
)
= ×
× +
+ ×
× +
+ ×
× =
= .
.
(5)设至少需n个乙这样的人,而n个乙这样的人译不出的概率为 n,故n个乙这样的人能译出的概率为1-
n,故n个乙这样的人能译出的概率为1- n≈99%.
n≈99%.
解得n=16.
故至少需16个乙这样的人,才能使译出的概率为99%.


科目:高中数学 来源: 题型:解答题
一个袋中装有5个形状大小完全相同的球,其中有2个红球,3个白球.
(1)从袋中随机取两个球,求取出的两个球颜色不同的概率;
(2)从袋中随机取一个球,将球放回袋中,然后再从袋中随机取一个球,求两次取出的球中至少有一个红球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某广场上有4盏装饰灯,晚上每盏灯都随机地闪烁红灯或绿灯,每盏灯出现红灯的概率都是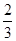 ,出现绿灯的概率都是
,出现绿灯的概率都是 .记这4盏灯中出现红灯的数量为X,当这排装饰灯闪烁一次时:
.记这4盏灯中出现红灯的数量为X,当这排装饰灯闪烁一次时:
(1)求X=2时的概率;
(2)求X的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两人各进行3次射击,甲每次击中目标的概率为 ,乙每次击中目标的概率为
,乙每次击中目标的概率为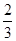 .
.
(1)求乙至多击中目标2次的概率;
(2)记甲击中目标的次数为Z,求Z的分布列、数学期望和标准差.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
抛掷红、蓝两颗骰子,设事件A为“蓝色骰子的点数为3或6”,事件B为“两颗骰子的点数之和大于8”.
(1)求P(A),P(B),P(AB);
(2)当已知蓝色骰子的点数为3或6时,求两颗骰子的点数之和大于8的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
有甲、乙两个盒子,甲盒子中有8张卡片,其中2张写有数字0,3张写有数字1,3张写有数字2;乙盒子中有8张卡片,其中3张写有数字0,2张写有数字1,3张写有数字2.
(1)如果从甲盒子中取2张卡片,从乙盒中取1张卡片,那么取出的3张卡片都写有1的概率是多少?
(2)如果从甲、乙两个盒子中各取1张卡片,设取出的两张卡片数字之和为X,求X的概率分布.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
齐王与田忌赛马,田忌的上马优于齐王的中马,劣于齐王的上马,田忌的中马优于齐王的下马,劣于齐王的中马,田忌的下马劣于齐王的下马,现各出上、中、下三匹马分组进行比赛.
(1) 如果双方均不知道对方马的出场顺序,求田忌获胜的概率;
(2) 为了得到更大的获胜概率,田忌预先了解到齐王第一场必出上等马.那么,田忌怎样安排出马顺序,才能使自己获胜的概率最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个口袋装有n个红球(n≥5且n∈N)和5个白球,一次摸奖从中摸2个球(每次摸奖后放回),2个球颜色不同则为中奖.
(1)试用n表示一次摸奖中奖的概率.
(2)若n=5,求3次摸奖的中奖次数ξ=1的概率及数学期望.
(3)记3次摸奖恰有1次中奖的概率为P,当n取多少时,P最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某小组共有A、B、C、D、E五位同学,他们的身高(单位:m)以及体重指标(单位:kg/m2)如下表所示:
| | A | B | C | D | E |
| 身高 | 1.69 | 1.73 | 1.75 | 1.79 | 1.82 |
| 体重指标 | 19.2 | 25.1 | 18.5 | 23.3 | 20.9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com