练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列说法：

    ①将一组数据中的每个数据都加上或减去同一个常数后，方差恒不变；

    ②设有一个回归方程，变量x增加一个单位时，y平均增加5个单位；

    ③线性回归方程必过（）；

    ④在一个2×2列联中，由计算得则有99%的把握确认这两个变量间有关系；

    ` 其中错误的个数是 （ ）

    本题可以参考独立性检验临界值表：


    0.5

    0.40

    0.25

    0.15

    0.10

    0.05

    0.25

    0.010

    0.005

    0.001

    k

    0.455

    0.708

    1.323

    2.072

    2.706

    3.841

    5.024

    6.535

    7.879

    10.828

    A.0B.1C.2D.3

    【答案】B

    【解析】

    ①根据方差的计算公式可知命题正确；②错，应为减少5个单位；③正确，这是回归直线方程满足的一个重要性质；④结合给出的数表，易知命题正确，故只有②是错误的．故选：B

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某蔬菜加工厂加工一种蔬菜，并对该蔬菜产品进行质量评级，现对甲、乙两台机器所加工的蔬菜产品随机抽取一部分进行评级，结果（单位：件）如表1：

    （1）若规定等级为合格等级，等级为优良等级，能否有的把握认为“蔬菜产品加工质量与机器有关”？

    （2）表2是用清水千克清洗该蔬菜千克后，该蔬菜上残留的农药微克的统计表，若用解析式作为与的回归方程，求出与的回归方程.（结果精确到）（参考数据：，，，.）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某中学为了丰富学生的课外文体活动，分别开设了阅读、书法、绘画等文化活动；跑步、游泳、健身操等体育活动．该中学共有高一学生300名，要求每位学生必须选择参加其中一项活动，现对高一学生的性别、学习积极性及选择参加的文体活动情况进行统计，得到数据如下：

    (1)在选择参加体育活动的学生中按性别分层抽取6名，再从这6名学生中抽取2人了解家庭情况，求2人中至少有1名女生的概率；

    (2)是否有99．9％的把握认为学生的学习积极性与选择参加文化活动有关?请说明你的理由．

    附：参考公式：，其中．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，P—ABCD是正四棱锥，是正方体，其中

    （1）求证：；

    （2）求平面PAD与平面所成的锐二面角的余弦值；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知双曲线： 的左、右焦点分别为， 为坐标原点， 是双曲线上在第一象限内的点，直线分别交双曲线左、右支于另一点， ，且，则双曲线的离心率为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】王府井百货分店今年春节期间，消费达到一定标准的顾客可进行一次抽奖活动，随着抽奖活动的有效开展，参与抽奖活动的人数越来越多，该分店经理对春节前7天参加抽奖活动的人数进行统计，表示第天参加抽奖活动的人数，得到统计表格如下：

    1

    2

    3

    4

    5

    6

    7

    5

    8

    8

    10

    14

    15

    17

    经过进一步统计分析，发现与具有线性相关关系.

    （1）请根据上表提供的数据，用最小二乘法求出关于的线性回归方程；

    （2）若该活动只持续10天，估计共有多少名顾客参加抽奖.

    参与公式：，，.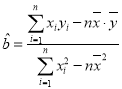

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2020年1月10日，引发新冠肺炎疫情的病毒基因序列公布后，科学家们便开始了病毒疫苗的研究过程.但是类似这种病毒疫苗的研制需要科学的流程，不是一朝一夕能完成的，其中有一步就是做动物试验.已知一个科研团队用小白鼠做接种试验，检测接种疫苗后是否出现抗体.试验设计是：每天接种一次，3天为一个接种周期.已知小白鼠接种后当天出现抗体的概率为，假设每次接种后当天是否出现抗体与上次接种无关.

    （1）求一个接种周期内出现抗体次数的分布列；

    （2）已知每天接种一次花费100元，现有以下两种试验方案：

    ①若在一个接种周期内连续2次出现抗体即终止本周期试验，进行下一接种周期，试验持续三个接种周期，设此种试验方式的花费为元；

    ②若在一个接种周期内出现2次或3次抗体，该周期结束后终止试验，已知试验至多持续三个接种周期，设此种试验方式的花费为元.本着节约成本的原则，选择哪种实验方案.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若直线l的极坐标方程为，曲线C的参数方程为(为参数)．

    若曲线上存在M，N两点关于直线l对称，求实数m的值；

    若直线与曲线相交于P，Q两点，且，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着经济的发展，个人收入的提高，自2019年1月1日起，个人所得税起征点和税率的调整.调整如下：纳税人的工资、薪金所得，以每月全部收入额减除5000元后的余额为应纳税所得额.依照个人所得税税率表，调整前后的计算方法如下表：

    个人所得税税率表（调整前）

    个人所得税税率表（调整后）

    免征额3500元

    免征额5000元

    级数

    全月应纳税所得额

    税率（%）

    级数

    全月应纳税所得额

    税率（%）

    1

    不超过1500元部分

    3

    1

    不超过3000元部分

    3

    2

    超过1500元至4500元的部分

    10

    2

    超过3000元至12000元的部分

    10

    3

    超过4500元至9000元的部分

    20

    3

    超过12000元至25000元的部分

    20

    ...

    ...

    ...

    ...

    ...

    ...

    （1）假如小红某月的工资、薪金等所得税前收入总和不高于8000元，记表示总收入，表示应纳的税，试写出调整前后关于的函数表达式；

    （2）某税务部门在小红所在公司利用分层抽样方法抽取某月100个不同层次员工的税前收入，并制成下面的频数分布表：

    收入（元）

    人数

    30

    40

    10

    8

    7

    5

    先从收入在及的人群中按分层抽样抽取7人，再从中选2人作为新纳税法知识宣讲员，求两个宣讲员不全是同一收入人群的概率；

    （3）小红该月的工资、薪金等税前收入为7500元时，请你帮小红算一下调整后小红的实际收入比调整前增加了多少？

    查看答案和解析>>

    同步练习册答案