
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 截以原点
截以原点![]() 为圆心的圆所得的弦长为
为圆心的圆所得的弦长为![]() 。
。
(1)求圆![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 切于第一象限,且与坐标轴交于点
切于第一象限,且与坐标轴交于点![]() ,当
,当![]() 长最小时,求直线
长最小时,求直线![]() 的方程;
的方程;
(3)设![]() 是圆
是圆![]() 上任意两点,点
上任意两点,点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,若直线
,若直线![]() 分别交
分别交![]() 轴于点
轴于点![]() 和
和![]() ,问
,问![]() 是否为定值?若是,请求出该定值;若不是,请说明理由。
是否为定值?若是,请求出该定值;若不是,请说明理由。
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】一房产商竞标得一块扇形![]() 地皮,其圆心角
地皮,其圆心角![]()
![]() ,半径为
,半径为![]()
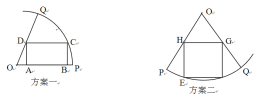
![]() ,房产商欲在此地皮上修建一栋平面图为矩形的商住楼,为使得地皮的使用率最大,准备了两种设计方案如图,方案一:矩形
,房产商欲在此地皮上修建一栋平面图为矩形的商住楼,为使得地皮的使用率最大,准备了两种设计方案如图,方案一:矩形![]() 的一边
的一边![]() 在半径
在半径![]() 上,
上,![]() 在圆弧上,
在圆弧上,![]() 在半径
在半径![]() ;方案二:矩形EFGH的顶点在圆弧上,顶点
;方案二:矩形EFGH的顶点在圆弧上,顶点![]() 分别在两条半径上。请你通过计算,为房产商提供决策建议。
分别在两条半径上。请你通过计算,为房产商提供决策建议。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为常数,且
为常数,且![]() .
.
(1)若![]() ,求函数
,求函数![]() 的表达式;
的表达式;
(2)在(1)的条件下,设函数![]() ,若
,若![]() 在区间[-2,2]上是单调函数,求实数
在区间[-2,2]上是单调函数,求实数![]() 的取值范围;
的取值范围;
(3)是否存在实数![]() 使得函数
使得函数![]() 在[-1,4]上的最大值是4?若存在,求出
在[-1,4]上的最大值是4?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装厂生产一种服装的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购超过100件时,每多订购1件,订购的全部服装的出场单价就降低0.02元,根据市场调查,销售商一次订购量不会超过600件.
(1)设销售一次订购![]() 件,服装的实际出厂单价为
件,服装的实际出厂单价为![]() 元,写出函数
元,写出函数![]() 的表达式;
的表达式;
(2)当销售商一次订购多少件服装时,该厂获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(重点班)我们知道对数函数![]() ,对任意
,对任意![]() ,都有
,都有![]() 成立,若
成立,若![]() ,则当
,则当![]() 时,
时,![]() .参照对数函数的性质,研究下题:定义在
.参照对数函数的性质,研究下题:定义在![]() 上的函数
上的函数![]() 对任意
对任意![]() ,都有
,都有![]() ,并且当且仅当
,并且当且仅当![]() 时,
时,![]() 成立.
成立.
(1)设![]() ,求证:
,求证:![]() ;
;
(2)设![]() ,若
,若![]() ,比较
,比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)若![]() ,求函数
,求函数![]() 的表达式;
的表达式;
(2)在(1)的条件下,设函数![]() ,若
,若![]() 上是单调函数,求实数
上是单调函数,求实数![]() 的取值范围;
的取值范围;
(3)是否存在![]() 使得函数
使得函数![]() 在
在![]() 上的最大值是4?若存在,求出
上的最大值是4?若存在,求出![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com