练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图所示，在三棱柱ABC－A1B1C1中，△ABC与△A1B1C1都为正三角形且AA1⊥面ABC，F、F1分别是AC，A1C1的中点．

    求证：(1)平面AB1F1∥平面C1BF；

    (2)平面AB1F1⊥平面ACC1A1.

    【答案】（1）见解析；（2）见解析.

    【解析】试题分析：（1）要证，只需证、，只需证、，而四边形、四边形皆为平行四边形，所以得证；（2）要证，只需证，只需证、，其中易知可得，△A1B1C1为正三角形可得，从而得证．

    试题解析：（1）连接，在三棱柱中，由为棱的中点，所以，四边形是平行四边形,所以,又,则.又在矩形中可得,且, ，则,而， 且，所以．

    （2）因为， ，所以，又因为△A1B1C1为正三角形， 的中点，所以，又，所以，因为，所以．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

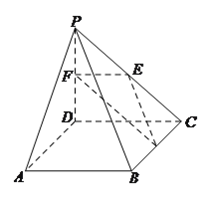
    【题目】如图，在四棱锥中， 是正方形， 平面， ， ， ， 分别是， ， 的中点．

    （）求四棱锥的体积．

    （）求证：平面平面．

    （）在线段上确定一点，使平面，并给出证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在三棱柱ABC﹣A1B1C1中，侧棱A1A⊥底面ABC，AC=1，AA1=2，∠BAC=90°，若直线AB1与直线A1C的夹角的余弦值是 ，则棱AB的长度是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随机变量ξ的分布列如表，其中a，b，c成等差数列．若E（ξ）= ，则D（ξ）=（ ）

    ξ

    1

    2

    3

    P

    a

    b

    c


    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等腰梯形中（如图1），， ， ， 为边上一点，且，将沿折起，使平面平面（如图2）.

    （1）证明：平面平面；

    （2）试在棱上确定一点，使截面把几何体分成的两部分.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，平面ABCD⊥平面ABEF，四边形ABCD是正方形，四边形ABEF是矩形，AF＝AD＝a，G是EF的中点．

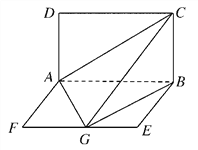
    (1)求证：平面AGC⊥平面BGC；

    (2)求GB与平面AGC所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题错误的是 （ ）

    A. 如果平面平面，那么平面内一定存在直线平行于平面

    B. 如果平面不垂直平面，那么平面内一定不存在直线垂直于平面

    C. 如果平面平面，平面平面，且，那么

    D. 如果平面平面，那么平面内所有直线都垂直于平面

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点A(0，3)，B(－1，0)，C(3，0)，求点D的坐标，使四边形ABCD为直角梯形(A，B，C，D按逆时针方向排列).

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列例子中随机变量ξ服从二项分布的有________．

    ①随机变量ξ表示重复抛掷一枚骰子n次中出现点数是3的倍数的次数；

    ②某射手击中目标的概率为0.9，从开始射击到击中目标所需的射击次数ξ；

    ③有一批产品共有N件，其中M件为次品，采用有放回抽取方法，ξ表示n次抽取中出现次品的件数（M<N）；

    ④有一批产品共有N件，其中M件为次品，采用不放回抽取方法，ξ表示n次抽取中出现次品的件数．

    查看答案和解析>>

    同步练习册答案