练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．在正方体ABCD-A1B1C1D1中，E为AB的中点，F为A1A的中点，则直线D1F与CE的位置关系是异面．（填平行、异面、相交三者之一）

    分析 取A1B1中点M，连结C1M，则CE∥C1M，由异面直线判定定理得D1F与C1M是异面直线，从而昨到直线D1F与CE的位置关系是异面．

    解答 解：取A1B1中点M，连结C1M，
    ∵在正方体ABCD-A1B1C1D1中，E为AB的中点，F为A1A的中点，
    ∴CE∥C1M，
    ∵FD1∩平面A1C1=D1，D1∉C1M，
    ∴由异面直线判定定理得D1F与C1M是异面直线，
    ∴直线D1F与CE的位置关系是异面．
    故答案为：异面．

    点评 本题考查两条直线的位置关系的判断，是基础题，解题时要认真审题，注意异面直线判定定理的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

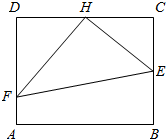    4．某高校专家楼前现有一块矩形草坪ABCD，已知草坪长AB=100米，宽BC=50$\sqrt{3}$米，为了便于专家平时工作、起居，该高校计划在这块草坪内铺设三条小路HE、HF和EF，并要求H是CD的中点，点E在边BC上，点F在边AD上，且∠EHF为直角，如图所示．
    （Ⅰ）设∠CHE=x（弧度），试将三条路的全长（即△HEF的周长）L表示成x的函数，并求出此函数的定义域；
    （Ⅱ）这三条路，每米铺设预算费用均为400元，试问如何设计才能使铺路的总费用最低？并求出最低总费用（结果保留整数）（可能用到的参考值：$\sqrt{3}$取1.732，$\sqrt{2}$取1.414）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知复数z=$\frac{2+i}{i^3}$，z的共轭复数是$\overline{z}$，则$\overline{z}$对应的点位于复平面内的（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．函数$y=\frac{{{{（x-1）}^0}}}{{\sqrt{|x|+x}}}$的定义域是（　　）
    A．（0，+∞）B．（0，1）∪（1，+∞）C．（-∞，0）D．（-∞，-1）∪（0，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．直线l的极坐标方程为ρcosθ-$\sqrt{3}$ρsinθ=5，圆C的参数方程为$\left\{\begin{array}{l}{x=5+2cosα}\\{y=4+2sinα}\end{array}\right.$（α为参数，α∈[0，2π）），则直线l与圆C的位置关系是（　　）
    A．相交B．相切C．相离D．无法确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．过点A（0，8）且与圆C：x2+y2+10x+10y=0相切于原点的圆的标准方程为（x-4）2+（y-4）2 =32．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．判断下列函数的奇偶性：
    （1）$f（x）=\frac{{{x^2}+1}}{{\sqrt{x+1}}}$；     
    （2）f（x）=|x+2|-|x-2|．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知$f（x）=\left\{{\begin{array}{l}{x-5}&{（x≤6）}\\{f（x+2）}&{（x＞6）}\end{array}}\right.$，则f（2011）等于（　　）
    A．0B．1C．2D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．如图，圆C与x轴相切于点T（1，0），与y轴正半轴交于两点A，B（B在A的上方），且|AB|=2．过点A任作一条直线与圆O：x2+y2=1相交于M，N两点，则$\frac{|NB|}{|NA|}$-$\frac{|MA|}{|MB|}$=2．

    查看答案和解析>>

    同步练习册答案