
【题目】袋子中有四张卡片,分别写有“瓷、都、文、明”四个字,有放回地从中任取一张卡片,将三次抽取后“瓷”“都”两个字都取到记为事件![]() ,用随机模拟的方法估计事件
,用随机模拟的方法估计事件![]() 发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
232 | 321 | 230 | 023 | 123 | 021 | 132 | 220 | 001 |
231 | 130 | 133 | 231 | 031 | 320 | 122 | 103 | 233 |
由此可以估计事件![]() 发生的概率为( )
发生的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
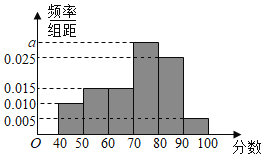
【题目】某校从高二年级学生中随机抽取60名学生,将期中考试的政治成绩(均为整数)分成六段:![]() 后得到如下频率分布直方图.
后得到如下频率分布直方图.
(1)根据频率分布直方图,分别求![]() ,众数,中位数。
,众数,中位数。
(2)估计该校高二年级学生期中考试政治成绩的平均分。
(3)用分层抽样的方法在各分数段的学生中抽取一个容量为20的样本,则在![]() 分数段抽取的人数是多少?
分数段抽取的人数是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二文科分四个班,各班人数恰好成等差数列,高二数学调研测试后,对四个文科班的学生试卷按每班人数进行分层抽样,对测试成绩进行统计,人数最少的班抽取了![]() 人,抽取的所有学生成绩分为
人,抽取的所有学生成绩分为![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图,其中第六组分数段的人数为
,得到如图所示的频率分布直方图,其中第六组分数段的人数为![]() 人.
人.
(![]() )求
)求![]() 的值,并求出各班抽取的学生数各为多少人?
的值,并求出各班抽取的学生数各为多少人?
(![]() )在抽取的学生中,任取一名学生,求分数不小于
)在抽取的学生中,任取一名学生,求分数不小于![]() 分的概率(视频率为概率).
分的概率(视频率为概率).
(![]() )估计高二文科四个班数学成绩的平均分
)估计高二文科四个班数学成绩的平均分

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C的内角对边分别为a,b,c,满足(a+b+c)(a﹣b+c)=ac.
(1)求B.
(2)若sinAsinC= ![]() ,求C.
,求C.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C: ![]() =1(a>0,b>0)的左、右焦点分别为F1 , F2 , 离心率为3,直线y=2与C的两个交点间的距离为
=1(a>0,b>0)的左、右焦点分别为F1 , F2 , 离心率为3,直线y=2与C的两个交点间的距离为 ![]() .
.
(1)求a,b;
(2)设过F2的直线l与C的左、右两支分别相交于A、B两点,且|AF1|=|BF1|,证明:|AF2|、|AB|、|BF2|成等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,D为边BC上一点,AD=6,BD=3, DC=2.
(1)若AD⊥BC,求∠BAC的大小;
(2)若∠ABC= ![]() ,求△ADC的面积.
,求△ADC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)袋中装有黑色球和白色球共7个,从中任取2个球都是白色球的概率为![]() .现有甲、乙两人从袋中轮流摸出1个球,甲先摸,乙后摸,然后甲再摸,……,摸后均不放回,直到有一人摸到白色球后终止.每个球在每一次被摸出的机会都是等可能的,用X表示摸球终止时所需摸球的次数.
.现有甲、乙两人从袋中轮流摸出1个球,甲先摸,乙后摸,然后甲再摸,……,摸后均不放回,直到有一人摸到白色球后终止.每个球在每一次被摸出的机会都是等可能的,用X表示摸球终止时所需摸球的次数.
(1)求随机变量X的分布列和均值E(X);
(2)求甲摸到白色球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com