
【题目】已知函数f(x)=ax2﹣x﹣lnx,a∈R.
(1)当 ![]() 时,求函数f(x)的最小值;
时,求函数f(x)的最小值;
(2)若﹣1≤a≤0,证明:函数f(x)有且只有一个零点;
(3)若函数f(x)有两个零点,求实数a的取值范围.
【答案】
(1)解:当 ![]() 时,
时, ![]() .
.
所以 ![]() ,(x>0).
,(x>0).
令f'(x)=0,得x=2,
当x∈(0,2)时,f'(x)<0;当x∈(2,+∞)时,f'(x)>0,
所以函数f(x)在(0,2)上单调递减,在(2,+∞)上单调递增.
所以当x=2时,f(x)有最小值 ![]()
(2)解:由f(x)=ax2﹣x﹣lnx,得 ![]() .
.
所以当a≤0时, ![]() ,
,
函数f(x)在(0,+∞)上单调递减,
所以当a≤0时,函数f(x)在(0,+∞)上最多有一个零点
因为当﹣1≤a≤0时,f(1)=a﹣1<0, ![]() ,
,
所以当﹣1≤a≤0时,函数f(x)在(0,+∞)上有零点.
综上,当﹣1≤a≤0时,函数f(x)有且只有一个零点
(3)解:由(2)知,当a≤0时,函数f(x)在(0,+∞)上最多有一个零点.
因为函数f(x)有两个零点,所以a>0.
由f(x)=ax2﹣x﹣lnx,得 ![]() ,令g(x)=2ax2﹣x﹣1.
,令g(x)=2ax2﹣x﹣1.
因为g(0)=﹣1<0,2a>0,
所以函数g(x)在(0,+∞)上只有一个零点,设为x0.
当x∈(0,x0)时,g(x)<0,f'(x)<0;当x∈(x0,+∞)时,g(x)>0,f'(x)>0.
所以函数f(x)在(0,x0)上单调递减;在(x0,+∞)上单调递增.
要使得函数f(x)在(0,+∞)上有两个零点,
只需要函数f(x)的极小值f(x0)<0,即 ![]() .
.
又因为 ![]() ,所以2lnx0+x0﹣1>0,
,所以2lnx0+x0﹣1>0,
又因为函数h(x)=2lnx+x﹣1在(0,+∞)上是增函数,且h(1)=0,
所以x0>1,得 ![]() .
.
又由 ![]() ,得
,得 ![]() ,
,
所以0<a<1. …13分
以下验证当0<a<1时,函数f(x)有两个零点.
当0<a<1时, ![]() ,
,
所以 ![]() .
.
因为 ![]() ,且f(x0)<0.
,且f(x0)<0.
所以函数f(x)在 ![]() 上有一个零点.
上有一个零点.
又因为 ![]() (因为lnx≤x﹣1),且f(x0)<0.
(因为lnx≤x﹣1),且f(x0)<0.
所以函数f(x)在 ![]() 上有一个零点.
上有一个零点.
所以当0<a<1时,函数f(x)在 ![]() 内有两个零点.
内有两个零点.
综上,实数a的取值范围为(0,1).
下面证明:lnx≤x﹣1.
设t(x)=x﹣1﹣lnx,所以 ![]() ,(x>0).
,(x>0).
令t'(x)=0,得x=1.
当x∈(0,1)时,t'(x)<0;当x∈(1,+∞)时,t'(x)>0.
所以函数t(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
所以当x=1时,t(x)有最小值t(1)=0.
所以t(x)=x﹣1﹣lnx≥0,得lnx≤x﹣1成立
【解析】(1)当 ![]() 时,
时, ![]() .求出函数的导数,得到极值点,然后判断单调性求解函数的最值.(2)由f(x)=ax2﹣x﹣lnx,得
.求出函数的导数,得到极值点,然后判断单调性求解函数的最值.(2)由f(x)=ax2﹣x﹣lnx,得 ![]() .当a≤0时,函数f(x)在(0,+∞)上最多有一个零点,当﹣1≤a≤0时,f(1)=a﹣1<0,
.当a≤0时,函数f(x)在(0,+∞)上最多有一个零点,当﹣1≤a≤0时,f(1)=a﹣1<0, ![]() ,推出结果.(3)由(2)知,当a≤0时,函数f(x)在(0,+∞)上最多有一个零点.说明a>0,由f(x)=ax2﹣x﹣lnx,得
,推出结果.(3)由(2)知,当a≤0时,函数f(x)在(0,+∞)上最多有一个零点.说明a>0,由f(x)=ax2﹣x﹣lnx,得 ![]() ,说明函数f(x)在(0,x0)上单调递减;在(x0 , +∞)上单调递增. 要使得函数f(x)在(0,+∞)上有两个零点,只需要
,说明函数f(x)在(0,x0)上单调递减;在(x0 , +∞)上单调递增. 要使得函数f(x)在(0,+∞)上有两个零点,只需要 ![]() .通过函数h(x)=2lnx+x﹣1在(0,+∞)上是增函数,推出0<a<1.验证当0<a<1时,函数f(x)有两个零点.证明:lnx≤x﹣1.
.通过函数h(x)=2lnx+x﹣1在(0,+∞)上是增函数,推出0<a<1.验证当0<a<1时,函数f(x)有两个零点.证明:lnx≤x﹣1.
设t(x)=x﹣1﹣lnx,利用导数求解函数的最值即可.
【考点精析】认真审题,首先需要了解函数的极值与导数(求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值).
是极小值).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》中有这样一个题目:“今有蒲生一日,长三尺;莞生一日,长一尺.蒲生日自半,莞生日自倍.问几何日而长等?”.其大意是“今有蒲生长1日,长为3尺;莞生长1日,长为1尺.蒲的生长逐日减其一半,莞的生长逐日增加一倍.问几日蒲、莞长度相等?”若本题改为求当蒲、莞长度相等时,莞的长度为( )
A. 4尺B. 5尺C. 6尺D. 7尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() ,圆Q:x2+y2﹣4x﹣2y+3=0的圆心Q在椭圆C上,点P(0,1)到椭圆C的右焦点的距离为2.
,圆Q:x2+y2﹣4x﹣2y+3=0的圆心Q在椭圆C上,点P(0,1)到椭圆C的右焦点的距离为2. 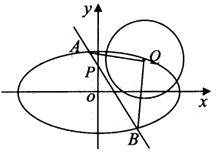
(1)求椭圆C的方程;
(2)过点P作直线l交椭圆C于A,B两点,若S△AQB=tan∠AQB,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高一某班级在学校数学嘉年华活动中推出了一款数学游戏,受到大家的一致追捧.游戏规则如下:游戏参与者连续抛掷一颗质地均匀的骰子,记第i次得到的点数为![]() ,若存在正整数n,使得
,若存在正整数n,使得![]() ,则称为游戏参与者的幸运数字。
,则称为游戏参与者的幸运数字。
(I)求游戏参与者的幸运数字为1的概率;
(Ⅱ)求游戏参与者的幸运数字为2的概率,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将圆的一组![]() 等分点分别涂上红色或蓝色,从任意一点开始,按逆时针方向依次记录
等分点分别涂上红色或蓝色,从任意一点开始,按逆时针方向依次记录![]() 个点的颜色,称为该圆的一个“
个点的颜色,称为该圆的一个“![]() 阶色序”,当且仅当两个“
阶色序”,当且仅当两个“![]() 阶色序”对应位置上的颜色至少有一个不相同时,称为不同的“
阶色序”对应位置上的颜色至少有一个不相同时,称为不同的“![]() 阶色序”.若某圆的任意两个“
阶色序”.若某圆的任意两个“![]() 阶色序”均不相同,则称该圆为“
阶色序”均不相同,则称该圆为“![]() 阶魅力圆”.“4阶魅力圆”中最多可有的等分点个数为__________.
阶魅力圆”.“4阶魅力圆”中最多可有的等分点个数为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 平面上,将两个半圆弧
平面上,将两个半圆弧![]() 和
和![]() 、两条直线
、两条直线![]() 和
和![]() 围成的封闭图形记为
围成的封闭图形记为![]() ,如图中阴影部分.记
,如图中阴影部分.记![]() 绕
绕![]() 轴旋转一周而成的几何体为
轴旋转一周而成的几何体为![]() ,过
,过![]() 作
作![]() 的水平截面,所得截面面积为
的水平截面,所得截面面积为![]() ,试利用祖暅原理(祖暅原理:“幂势既同,则积不容异”,意思是:两等高的几何体在同高处被截得的两个截面面积均相等,那么这两个几何体的体积相等)、一个平放的圆柱和一个长方体,得出
,试利用祖暅原理(祖暅原理:“幂势既同,则积不容异”,意思是:两等高的几何体在同高处被截得的两个截面面积均相等,那么这两个几何体的体积相等)、一个平放的圆柱和一个长方体,得出![]() 的体积值为__________.
的体积值为__________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}前n项和Sn满足:2Sn+an=1.
(1)求数列{an}的通项公式;
(2)设 ![]() ,数列{bn}的前n项和为Tn , 求证:Tn<2.
,数列{bn}的前n项和为Tn , 求证:Tn<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自2016年1月1日起,我国全面二孩政策正式实施,这次人口与生育政策的历史性调整,使得“要不要再生一个”“生二孩能休多久产假”等成为千千万万个家庭在生育决策上避不开的话题.为了解针对产假的不同安排方案形成的生育意愿,某调查机构随机抽取了200户有生育二胎能力的适龄家庭进行问卷调查,得到如下数据:
产假安排(单位:周) | 14 | 15 | 16 | 17 | 18 |
有生育意愿家庭数 | 4 | 8 | 16 | 20 | 26 |
(1)若用表中数据所得的频率代替概率,面对产假为14周与16周,估计某家庭有生育意愿的概率分别为多少?
(2)假设从5种不同安排方案中,随机抽取2种不同安排分别作为备选方案,然后由单位根据单位情况自主选择. ①求两种安排方案休假周数和不低于32周的概率;
②如果用ξ表示两种方案休假周数和.求随机变量ξ的分布及期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com