
【题目】如图,由于函数f(x)=sin(π﹣ωx)sin( ![]() +φ)﹣sin(ωx+
+φ)﹣sin(ωx+ ![]() )sinφ(ω>0)的图象部分数据已污损,现可以确认点C(
)sinφ(ω>0)的图象部分数据已污损,现可以确认点C( ![]() ,0),其中A点是图象在y轴左侧第一个与x轴的交点,B点是图象在y轴右侧第一个最高点,则f(x)在下列区间中是单调的( )
,0),其中A点是图象在y轴左侧第一个与x轴的交点,B点是图象在y轴右侧第一个最高点,则f(x)在下列区间中是单调的( ) 
A.(0, ![]() )
)
B.( ![]() ,
, ![]() )
)
C.( ![]() ,2π)
,2π)
D.( ![]() ,
, ![]() )
)
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0),离心率为
=1(a>b>0),离心率为 ![]() ,两焦点分别为F1、F2 , 过F1的直线交椭圆C于M,N两点,且△F2MN的周长为8.
,两焦点分别为F1、F2 , 过F1的直线交椭圆C于M,N两点,且△F2MN的周长为8.
(1)求椭圆C的方程;
(2)过点P(m,0)作圆x2+y2=1的切线l交椭圆C于A,B两点,求弦长|AB|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PD⊥底面ABCD,且底面ABCD为平行四边形,若∠DAB=60°,AB=2,AD=1. 
(1)求证:PA⊥BD;
(2)若∠PCD=45°,求点D到平面PBC的距离h.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A1 , A2为椭圆 ![]() =1的长轴的左、右端点,O为坐标原点,S,Q,T为椭圆上不同于A1 , A2的三点,直线QA1 , QA2 , OS,OT围成一个平行四边形OPQR,则|OS|2+|OT|2=( )
=1的长轴的左、右端点,O为坐标原点,S,Q,T为椭圆上不同于A1 , A2的三点,直线QA1 , QA2 , OS,OT围成一个平行四边形OPQR,则|OS|2+|OT|2=( ) 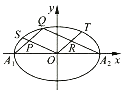
A.5
B.3+ ![]()
C.9
D.14
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别是AB,BC的中点.将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于P. 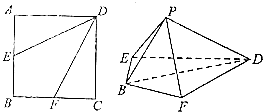
(1)求证:平面PBD⊥平面BFDE;
(2)求二面角P﹣DE﹣F的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解市民在购买食物时看营养说明与性别的关系,现在社会上随机询问了100名市民,得到如下2×2列联表:
(1)是否有95%的把握认为:“性别与读营养说明有关系”,并说明理由;
(2)把频率当概率,若从社会上的男性市民中随机抽取3位,记这3位中读营养说明的人数为ξ,求随机变量ξ的分布列和数学期望E(ξ).
男性 | 女性 | 总计 | |
读营养说明 | 40 | 20 | 60 |
不读营养说明 | 20 | 20 | 40 |
总计 | 60 | 40 | 100 |
参考公式和数据: ![]()
P(K2≥k0) | 0.10 | 0.050 | 0.025 | 0.010 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数F(x)= ![]() ,(a为实数).
,(a为实数).
(1)根据a的不同取值,讨论函数y=f(x)的奇偶性,并说明理由;
(2)若对任意的x≥1,都有1≤f(x)≤3,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合Ma={f(x)|存在正实数a,使得定义域内任意x都有f(x+a)>f(x)}.
(1)若f(x)=2x﹣x2 , 试判断f(x)是否为M1中的元素,并说明理由;
(2)若 ![]() ,且g(x)∈Ma , 求a的取值范围;
,且g(x)∈Ma , 求a的取值范围;
(3)若 ![]() (k∈R),且h(x)∈M2 , 求h(x)的最小值.
(k∈R),且h(x)∈M2 , 求h(x)的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com