Question

13．已知圆C：x²+y²+2x-4y+3=0．
（1）直线l过点（-2，0）且被圆C截得的弦长为2，求直线l的方程；
（2）从圆C外一点P向圆引一条切线，切点为M，O为坐标原点，且有|PM|=|PO|，求|PM|的最小值．

Answer 1

分析 （1）⊙C：x²+y²+2x-4y+3=0，化为标准方程，求出圆心C，半径r．分类讨论，利用C到l的距离为1，即可求直线l的方程；
（2）设P（x，y）．由切线的性质可得：CM⊥PM，利用|PM|=|PO|，可得3x+4y-12=0，求|PM|的最小值，即求|PO|的最小值，即求原点O到直线2x-4y+3=0的距离

解答 解：（1）x²+y²+2x-4y+3=0可化为（x+1）²+（y-2）²=2
当l的斜率不存在时，其方程为x=-2，与圆C的交点为A（-2，1），B（-2，3）
|AB|=2，符合题意   …（2分）
当l的斜率存在时，设其方程为y=k（x+2）即kx-y+2k=0
则C到l的距离$d=\frac{{|{-k-2+2k}|}}{{\sqrt{{k^2}+1}}}=1$
解得$k=\frac{3}{4}$，∴l的方程为3x-4y+6=0
综上，直线l的方程为x=-2或3x-4y+6=0…（6分）
（2）如图：PM为圆C的切线，则CM⊥PM，∴△PMC为直角三角形，∴|PM|²=|PC|²-|MC|²．
设P（x，y），C（-1，2），|MC|=$\sqrt{2}$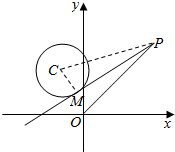

∵|PM|=|PO|，
∴x²+y²=（x+1）²+（y-2）²-2．
化简得点P的轨迹方程为2x-4y+3=0．
求|PM|的最小值，即求|PO|的最小值，即求原点O到直线2x-4y+3=0的距离，代入点到直线的距离公式可求得|PM|最小值为$\frac{{3\sqrt{5}}}{10}$…（12分）

点评 本题考查直线方程，考查直线与圆的位置关系，考查了圆的切线的性质、勾股定理、两点之间的距离公式，考查了推理能力与计算能力，属于中档题．