
【题目】研究表明某地的山高![]() (
(![]() )与该山的年平均气温
)与该山的年平均气温![]() (
(![]() )具有相关关系,根据所采集的数据得到线性回归方程
)具有相关关系,根据所采集的数据得到线性回归方程![]() ,则下列说法错误的是( )
,则下列说法错误的是( )
A.年平均气温为![]() 时该山高估计为
时该山高估计为![]()
B.该山高为![]() 处的年平均气温估计为
处的年平均气温估计为![]()
C.该地的山高![]() 与该山的年平均气温
与该山的年平均气温![]() 的正负相关性与回归直线的斜率的估计值有关
的正负相关性与回归直线的斜率的估计值有关
D.该地的山高![]() 与该山的年平均气温
与该山的年平均气温![]() 成负相关关系
成负相关关系
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,已知曲线![]() ,以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线l:p(2cosθ-sinθ)=6.
,以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线l:p(2cosθ-sinθ)=6.
(1)试写出直线l的直角坐标方程和曲线C1的参数方程;
(2)在子曲线C1上求一点P,使点P到直线l的距离最大,并求出此最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面![]() 与平面
与平面![]() 平行的充分条件可以是( )
平行的充分条件可以是( )
A.![]() 内有无穷多条直线都与
内有无穷多条直线都与![]() 平行
平行
B.直线![]() ,
,![]() ,且直线a不在
,且直线a不在![]() 内,也不在
内,也不在![]() 内
内
C.直线![]() ,直线
,直线![]() ,且
,且![]() ,
,![]()
D.![]() 内的任何一条直线都与
内的任何一条直线都与![]() 平行
平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快餐连锁店招聘外卖骑手,该快餐连锁店提供了两种日工资方案:方案①:规定每日底薪50元,快递业务每完成一单提成3元;方案②:规定每日底薪100元,快递业务的前44单没有提成,从第45单开始,每完成一单提成5元.该快餐连锁店记录了每天骑手的人均业务量.现随机抽取100天的数据,将样本数据分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 七组,整理得到如图所示的频率分布直方图.
七组,整理得到如图所示的频率分布直方图.
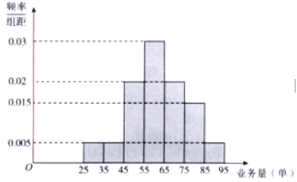
(1)随机选取一天,估计这一天该连锁店的骑手的人均日快递业务量不少于65单的概率;
(2)若骑手甲、乙选择了日工资方案①,丙、丁选择了日工资方案②.现从上述4名骑手中随机选取2人,求至少有1名骑手选择方案①的概率;
(3)若从人均日收入的角度考虑,请你利用所学的统计学知识为新聘骑手做出日工资方案的选择,并说明理由.(同组中的每个数据用该组区间的中点值代替)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校要从甲、乙两名同学中选择一人参加该市组织的数学竞赛,已知甲、乙两名同学最近7次模拟竞赛的数学成绩(满分100分)如下:
甲:79,81,83,84,85,90,93;
乙:75,78,82,84,90,92,94.
(1)完成答题卡中的茎叶图;
(2)分别计算甲、乙两名同学最近7次模拟竞赛成绩的平均数与方差,并由此判断该校应选择哪位同学参加该市组织的数学竞赛.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ,给出下列关于
,给出下列关于![]() 的性质:
的性质:
①![]() 是周期函数,3是它的一个周期;
是周期函数,3是它的一个周期;
②![]() 是偶函数;
是偶函数;
③方程![]() 有有理根;
有有理根;
④方程![]() 与方程
与方程![]() 的解集相同;
的解集相同;
⑤![]() 是周期函数,
是周期函数,![]() 是它的一个周期.
是它的一个周期.
其中正确的个数为( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com