
| A. | x=-$\frac{π}{6}$ | B. | x=$\frac{π}{3}$ | C. | x=-$\frac{π}{12}$ | D. | x=$\frac{π}{12}$ |
分析 由条件根据函数y=Asin(ωx+φ)的图象变换规律,可得结论.
解答 解:由题意得:把y=sinx的图象所有点的横坐标变为原来的$\frac{1}{2}$倍得到y=sin2x的图象,
把y=sin2x的图象向左平移$\frac{π}{6}$个单位可得y=sin[2(x+$\frac{π}{6}$)]=sin(2x+$\frac{π}{3}$)的图象,
故:y=sin(2x+$\frac{π}{3}$),
由题意可得:2x+$\frac{π}{3}$=$\frac{π}{2}$,解得:x=$\frac{π}{12}$.
故选:D.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $a>\sqrt{19}或a<-\sqrt{19}或-\sqrt{3}<a<\sqrt{3}$ | B. | $2<a<\frac{8}{3}$ | ||
| C. | $-1<a<\frac{8}{3}$ | D. | a∈∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{2}$ | B. | 4 | C. | $\frac{9}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{5}$ | B. | -$\frac{\sqrt{2}}{5}$ | C. | $\frac{\sqrt{2}}{10}$ | D. | -$\frac{\sqrt{2}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
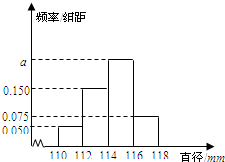 某工厂生产的产品A的直径均位于区间[110,118]内(单位:mm).若生产一件产品A的直径位于区间[110,112),[112,114),[114,116),[116,118]内该厂可获利分别为10,30,20,10(单位:元),现从该厂生产的产品A中随机抽取200件测量它们的直径,得到如图所示的频率分布直方图.
某工厂生产的产品A的直径均位于区间[110,118]内(单位:mm).若生产一件产品A的直径位于区间[110,112),[112,114),[114,116),[116,118]内该厂可获利分别为10,30,20,10(单位:元),现从该厂生产的产品A中随机抽取200件测量它们的直径,得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{25}{3}$ | B. | $\frac{50}{9}$ | C. | 7 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com