
【题目】已知二次函数f(x)满足f(x+1)-f(x)=-2x+1,且f(2)=15.
(1)求函数f(x)的解析式;
(2) 令g(x)=(2-2m)x-f(x).
① 若函数g(x)在x∈[0,2]上是单调函数,求实数m的取值范围;
② 求函数g(x)在x∈[0,2]上的最小值.
【答案】(1)f(x)=-x2+2x+15.(2)①m≤0或m≥2. ②见解析
【解析】试题分析:(1)设二次函数一般式f(x)=ax2+bx+c(a≠0),代入条件化简,根据恒等条件得2a=-2,a+b=1,解得a=-1,b=2.再根据f(2)=15,求c(2)①根据二次函数对称轴必在定义区间外得实数m的取值范围;②根据对称轴与定义区间位置关系,分三种情况讨论函数最小值取法.
试题解析:解:(1) 设二次函数f(x)=ax2+bx+c(a≠0),
则f(x+1)-f(x)=a(x+1)2+b(x+1)+c-(ax2+bx+c)=2ax+a+b=-2x+1,
∴ 2a=-2,a+b=1,∴ a=-1,b=2.
又f(2)=15,∴ c=15.
∴ f(x)=-x2+2x+15.
(2) ① ∵ f(x)=-x2+2x+15,
∴ g(x)=(2-2m)x-f(x)=x2-2mx-15.
又g(x)在x∈[0,2]上是单调函数,∴ 对称轴x=m在区间[0,2]的左侧或右侧,∴ m≤0或m≥2.
② g(x)=x2-2mx-15,x∈[0,2],对称轴x=m,
当m>2时,g(x)min=g(2)=4-4m-15=-4m-11;
当m<0时,g(x)min=g(0)=-15;
当0≤m≤2时,g(x)min=g(m)=m2-2m2-15=-m2-15.
综上所述,g(x)min=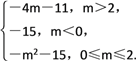


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知AD=4, ![]() ,AB=2CD=8.
,AB=2CD=8.
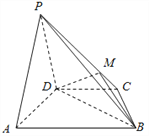
(1)设M是PC上的一点,证明:平面MBD⊥平面PAD;
(2)当M点位于线段PC什么位置时,PA∥平面MBD?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】3名志愿者在10月1号至10月5号期间参加社区服务工作.
(1)若每名志愿者在这5天中任选一天参加社区服务工作,且各志愿者的选择互不影响,求3名志愿者恰好连续3天参加社区服务工作的概率;
(2)若每名志愿者在这5天中任选两天参加社区服务工作,且各志愿者的选择互不影响,记![]() 表示这3名志愿者在10月1号参加社区服务工作的人数,求随机变量
表示这3名志愿者在10月1号参加社区服务工作的人数,求随机变量![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
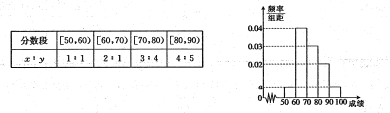
【题目】某校100名学生其中考试语文成绩的频率分布直方图所示,其中成绩分组区间是:
![]() .
.
(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文某些分数段的人数![]() 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数![]() 之比如下表所示,
之比如下表所示,
求数学成绩在![]() 之外的人数.
之外的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,以
,以![]() 为圆心,椭圆的短半轴长为半径的圆与直线
为圆心,椭圆的短半轴长为半径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知点![]() ,和平面内一点
,和平面内一点![]() (
(![]() ),过点
),过点![]() 任作直线
任作直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,设直线
两点,设直线![]() ,
,![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() ,
,![]() ,试求
,试求![]() ,
,![]() 满足的关系式.
满足的关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com