
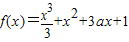 ,动直线l的斜率k=2.
,动直线l的斜率k=2. ),
), =2(x+1),即:2x+y+
=2(x+1),即:2x+y+ =0;
=0;

科目:高中数学 来源: 题型:
| x3 | 3 |
查看答案和解析>>
科目:高中数学 来源:河北省邯郸市临漳一中2012届高三春季开学摸底考试数学文科试题 题型:022
下列四个命题:
①若m∈(0,1],则函数![]() 的最小值为
的最小值为![]() ;
;
②已知平面α,β,直线l,m,若l⊥α,m![]() β,α⊥β,则l∥m;
β,α⊥β,则l∥m;
③△ABC中![]() 和
和![]() 的夹角等于180°-A;
的夹角等于180°-A;
④若动点P到点F(1,0)的距离比到直线l:x=-2的距离小1,则动点P的轨迹方程为y2=4x.
其中正确命题的序号为________.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
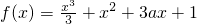 ,动直线l的斜率k=2.
,动直线l的斜率k=2.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| x3 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com