
【题目】如图,矩形![]() 所在的平面与正方形
所在的平面与正方形![]() 所在的平面相互垂直,
所在的平面相互垂直,![]() 是
是![]() 的中点.
的中点.
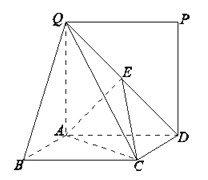
(Ⅰ)求证:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(Ⅲ)若![]() ,
,![]() ,求多面体
,求多面体![]() 的体积.
的体积.
【答案】(Ⅰ)详见解析(Ⅱ)详见解析(Ⅲ)1
【解析】
试题(Ⅰ)连接BD交AC于O,连接EO.证明EO∥QB,即可证明QB∥平面AEC;(Ⅱ)证明CD⊥AE,AE⊥QD.推出AE⊥平面QDC,然后证明平面QDC⊥平面AEC;(Ⅲ)通过多面体ABCEQ为四棱锥Q-ABCD截去三棱锥E-ACD所得,计算求解即可
试题解析:(Ⅰ)证明:连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
因为 ![]() 分别为
分别为![]() 和
和![]() 的中点,则
的中点,则![]() ∥
∥![]() .
.
又 ![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以 ![]() ∥平面
∥平面![]()
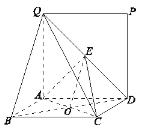
(Ⅱ)证明: 因为矩形![]() 所在的平面与正方形
所在的平面与正方形![]() 所在的平面相互垂直,
所在的平面相互垂直,
![]() 平面
平面![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() , 所以
, 所以![]() .
.
因为![]() ,
,![]() 是
是![]() 的中点, 所以
的中点, 所以![]() .
.
所以![]() 平面
平面![]() .
.
所以平面![]() ⊥平面
⊥平面![]() .
.
(Ⅲ)解:多面体![]() 为四棱锥
为四棱锥![]() 截去三棱锥
截去三棱锥![]() 所得,
所得,
所以![]() .
.


 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为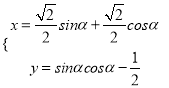 (
(![]() 为参数),若以直角坐标系中的原点为极点,
为参数),若以直角坐标系中的原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() 为实数.)
为实数.)
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 与曲线
与曲线![]() 有公共点,求
有公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医疗器械公司在全国共有![]() 个销售点,总公司每年会根据每个销售点的年销量进行评价分析.规定每个销售点的年销售任务为一万四千台器械.根据这
个销售点,总公司每年会根据每个销售点的年销量进行评价分析.规定每个销售点的年销售任务为一万四千台器械.根据这![]() 个销售点的年销量绘制出如下的频率分布直方图.
个销售点的年销量绘制出如下的频率分布直方图.

(1)完成年销售任务的销售点有多少个?
(2)若用分层抽样的方法从这![]() 个销售点中抽取容量为
个销售点中抽取容量为![]() 的样本,求该五组
的样本,求该五组![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,(单位:千台)中每组分别应抽取的销售点数量.
,(单位:千台)中每组分别应抽取的销售点数量.
(3)在(2)的条件下,从该样本中完成年销售任务的销售点中随机选取![]() 个,求这两个销售点不在同一组的概率.
个,求这两个销售点不在同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有2名男生、3名女生,全体排成一行,问下列情形各有多少种不同的排法?(以下各题请用数字作答)
(1)甲不在中间也不在两端;
(2)甲、乙两人必须排在两端;
(3)男、女生分别排在一起;
(4)男女相间;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况.下列叙述中正确的是( )
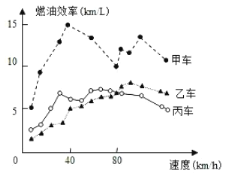
A.消耗1升汽油,乙车最多可行驶5千米
B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C.甲车以80千米/小时的速度行驶1小时,消耗8升汽油
D.某城市机动车最高限速80千米/小时.相同条件下,在该市用乙车比用丙车更省油
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知点
中,已知点![]() ,圆
,圆![]() :
:![]() 与
与![]() 轴的正半轴的交点是
轴的正半轴的交点是![]() ,过点
,过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() .
.

(1)若直线![]() 与
与![]() 轴交于
轴交于![]() ,且
,且![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设直线![]() ,
,![]() 的斜率分别是
的斜率分别是![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)设![]() 的中点为
的中点为![]() ,点
,点![]() ,若
,若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一块半圆形的空地,直径![]() 米,政府计划在空地上建一个形状为等腰梯形的花圃
米,政府计划在空地上建一个形状为等腰梯形的花圃![]() ,如图所示,其中
,如图所示,其中![]() 为圆心,
为圆心,![]() ,
,![]() 在半圆上,其余为绿化部分,设
在半圆上,其余为绿化部分,设![]() .
.

(1)记花圃的面积为![]() ,求
,求![]() 的最大值;
的最大值;
(2)若花圃的造价为10元/米,在花圃的边![]() 、
、![]() 处铺设具有美化效果的灌溉管道,铺设费用为500元/米,两腰
处铺设具有美化效果的灌溉管道,铺设费用为500元/米,两腰![]() 、
、![]() 不铺设,求
不铺设,求![]() 满足什么条件时,会使总造价最大.
满足什么条件时,会使总造价最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com