
分析 (Ⅰ)射线l:θ=$\frac{π}{6}$与圆C:ρ=2交于点A(2,$\frac{π}{6}$),可得点A的直角坐标;求出椭圆直角坐标方程,即可求出椭圆Γ的参数方程;
(Ⅱ)设F($\sqrt{3}$cosθ,sinθ),E(0,-1),求出相应的向量,即可求$\overrightarrow{AE}$•$\overrightarrow{AF}$的取值范围.
解答 解:(Ⅰ)射线l:θ=$\frac{π}{6}$与圆C:ρ=2交于点A(2,$\frac{π}{6}$),点A的直角坐标($\sqrt{3}$,1);
椭圆Γ的方程为ρ2=$\frac{3}{1+2si{n}^{2}θ}$,直角坐标方程为$\frac{{x}^{2}}{3}$+y2=1,参数方程为$\left\{\begin{array}{l}{x=\sqrt{3}cosθ}\\{y=sinθ}\end{array}\right.$(θ为参数);
(Ⅱ)设F($\sqrt{3}$cosθ,sinθ),
∵E(0,-1),
∴$\overrightarrow{AE}$=(-$\sqrt{3}$,-2),$\overrightarrow{AF}$=($\sqrt{3}$cosθ-$\sqrt{3}$,sinθ-1),
∴$\overrightarrow{AE}$•$\overrightarrow{AF}$=-3cosθ+3-2(sinθ-1)=$\sqrt{13}$sin(θ+α)+5,
∴$\overrightarrow{AE}$•$\overrightarrow{AF}$的取值范围是[5-$\sqrt{13}$,5+$\sqrt{13}$].
点评 本题考查极坐标方程、直角坐标方程、参数方程的转化,考查向量的数量积公式,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
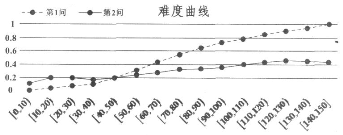
| A. | 此题没有考生得12分 | |
| B. | 此题第1问比第2问更能区分学生数学成绩的好与坏 | |
| C. | 分数在[40,50)的考生此大题的平均得分大约为4.8分 | |
| D. | 全体考生第1问的得分标准差小于第2问的得分标准差 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com