
【题目】某兴趣小组为调查当地居民的收入水平,他们对当地一个有5000人的社区随机抽取1000人,调查他们的月收入,根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)),因操作人员不慎,未标出第五组顶部对应的纵轴数据.
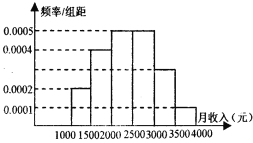
(Ⅰ)请你补上第五组顶部对应的纵轴数据,并估算该社区居民月收入在[3000,4000)的人数;
(Ⅱ)根据频率分布直方图估算样本数据的中位数;
(Ⅲ)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这1000人中用分层抽样方法抽出100人作进一步分析,则月收入在[2500,3000)的这段应抽多少人?
【答案】(I)![]() 人;(II)
人;(II)![]() ;(III)
;(III)![]() 人.
人.
【解析】
试题分析:(I)根据频率分布直方图可知,每个小长方形的面积表示该组的频率,所有小长方形面积之和等于![]() ,第五组的频率为
,第五组的频率为![]() ,所以根据频率分布直方图可知,该社区居民月收入在
,所以根据频率分布直方图可知,该社区居民月收入在![]() 的人数应为
的人数应为![]() ;(II)根据频率分布直方图的性质可知,中位数在小长方形面积和即频率和等于
;(II)根据频率分布直方图的性质可知,中位数在小长方形面积和即频率和等于![]() 处所对应的横坐标数据,第一组频率为
处所对应的横坐标数据,第一组频率为![]() ,第二组频率为
,第二组频率为![]() ,第三组频率为
,第三组频率为![]() ,前两组频率和为
,前两组频率和为![]() ,因为
,因为![]() ,所以中位数在第三组横坐标的
,所以中位数在第三组横坐标的![]() 处,即中位数为
处,即中位数为![]() ;(III)根据分层抽样的性质可知,月收入在
;(III)根据分层抽样的性质可知,月收入在![]() 这段的频率为
这段的频率为![]() ,设在此段内抽取的人数为
,设在此段内抽取的人数为![]() ,则有
,则有![]() ,所以
,所以![]() ,则应抽取
,则应抽取![]() 人.
人.
试题解析:(I)第五组顶部对应的纵轴数据为:0.0003
居民收入在![]() 的人数为
的人数为
![]() (人) 4分
(人) 4分
(II)第一组和第二组的频率之和为(0.0002+0.0004)![]() 500=0.3
500=0.3
第三组的频率为0.0005![]() 500=.25
500=.25
因此,可以估算样本数据的中位数为![]() (元) 8分
(元) 8分
(III)第四组的人数为0.0005 ![]() 500
500![]() 1000=250
1000=250
因此月收入在![]() 的这段应抽
的这段应抽![]() (人) 12分
(人) 12分


科目:高中数学 来源: 题型:
【题目】已知a、b、c是互不相等的非零实数.若用反证法证明三个方程ax2+2bx+c=0,bx2+2cx+a=0,cx2+2ax+b=0至少有一个方程有两个相异实根,应假设成( )
A. 三个方程都没有两个相异实根 B. 一个方程没有两个相异实根
C. 至多两个方程没有两个相异实根 D. 三个方程不都没有两个相异实根
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).若直线
为参数).若直线![]() 与圆
与圆![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() .
.
(Ⅰ)写出圆![]() 的直角坐标方程,并求圆心的坐标与半径;
的直角坐标方程,并求圆心的坐标与半径;
(Ⅱ)若弦长![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com