【题目】在平面直角坐标系xOy中，点A（﹣1，﹣2）、B（2，3）、C（﹣2，﹣1）．
（1）求以线段AB、AC为邻边的平行四边形两条对角线的长；
（2）设实数t满足（ 
） 
=0，求t的值．
【答案】
（1）解：（方法一）由题设知 
，则 
．
所以 
．
故所求的两条对角线的长分别为 
、 
．
（方法二）设该平行四边形的第四个顶点为D，两条对角线的交点为E，则：
E为B、C的中点，E（0，1）
又E（0，1）为A、D的中点，所以D（1，4）
故所求的两条对角线的长分别为BC= 、AD=
（2）解：由题设知： 
=（﹣2，﹣1）， 
．
由（ 
） =0，得：（3+2t，5+t）（﹣2，﹣1）=0，
从而5t=﹣11，所以 
．
或者： 
， 
， 
【解析】（1）（方法一）由题设知 ，则 ．从而得： ．（方法二）设该平行四边形的第四个顶点为D，两条对角线的交点为E，则：由E是AC，BD的中点，易得D（1，4）从而得：BC= 、AD= ；（2）由题设知： =（﹣2，﹣1）， ．由（ ） =0，得：（3+2t，5+t）（﹣2，﹣1）=0，从而得： ．或者由 
， ，得：
千里马走向假期期末仿真试卷寒假系列答案科目：高中数学 来源： 题型：
【题目】已知函数f（x）=|x﹣a|，g（x）=ax，（a∈R）．
（1）若函数y=f（x）是偶函数，求出符合条件的实数a的值；
（2）若方程f（x）=g（x）有两解，求出实数a的取值范围；
（3）若a＞0，记F（x）=g（x）f（x），试求函数y=F（x）在区间[1，2]上的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=sin2x+2 
sin2x+1﹣ ．
（1）求函数f（x）的最小正周期和单调递增区间；
（2）当x∈[ 
， 
]时，求函数f（x）的值域．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数f（x）=loga（x﹣3a）（a＞0且a≠1），当点P（x，y）是函数y=f（x）图象上的点时，点
Q（x﹣2a，﹣y）是函数y=g（x）图象上的点．
（1）写出函数y=g（x）的解析式；
（2）若当x∈[a+2，a+3]时，恒有|f（x）﹣g（x）|≤1，试确定a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在棱长为a的正方体ABCD﹣A1B1C1D1中，E、F分别是AB、BC的中点，EF与BD交于点G，M为棱BB1上一点．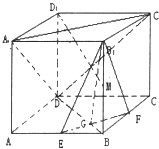 
（1）证明：EF∥平面 A1C1D；
（2）当B1M：MB的值为多少时，D1M⊥平面 EFB1 ， 证明之；
（3）求点D到平面 EFB1的距离．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知y=f（x+1）是定义在R上的周期为2的偶函数，当x∈[1，2）时，f（x）=log2x，设a=f（ 
）， 
，c=f（1），则a，b，c的大小关系为（ ）
A.a＜c＜b
B.c＜a＜b
C.b＜c＜a
D.c＜b＜a
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
