
分析 (1)进行数量积的坐标运算,并化简可得到$\overrightarrow{a}•\overrightarrow{b}=2cos(α+β)=-\frac{10}{13}$,根据α,β的范围即可求出sin(α+β)的值,而根据$sinβ=\frac{4}{5}$及β的范围即可求出cosβ的值,而sin(α+2β)=sin[(α+β)+β],这样根据两角和的正弦公式即可求出sin(α+2β)的值;
(2)先求出$\overrightarrow{a}-\overrightarrow{c}$的坐标,从而求出$|\overrightarrow{a}-\overrightarrow{c}|=\sqrt{3si{n}^{2}α-4sinα+2}$,换元sinα=t,t∈[0,1],从而得出$|\overrightarrow{a}-\overrightarrow{c}|=\sqrt{3{t}^{2}-4t+2}$,这样配方即可求出$|\overrightarrow{a}-\overrightarrow{c}|$的取值范围.
解答 解:(1)$\overrightarrow a•\overrightarrow b=2cosαcosβ-2sinαsinβ$=$2cos(α+β)=-\frac{10}{13}$;
∴$cos(α+β)=-\frac{5}{13}$;
∵0≤α+β≤π;
∴$sin(α+β)=\sqrt{1-{{cos}^2}(α+β)}=\frac{12}{13}$;
又 $sinβ=\frac{4}{5}$,$β∈[0,\frac{π}{2}]$,$cosβ=\frac{3}{5}$;
∴sin(α+2β)=sin[(α+β)+β]
=sin(α+β)cosβ+cos(α+β)sinβ
=$\frac{12}{13}×\frac{3}{5}-\frac{5}{13}×\frac{4}{5}$
=$\frac{16}{65}$;
(2)由已知得:$\overrightarrow a-\overrightarrow c=(cosα,2sinα-1)$;
∴$|{\overrightarrow a-\overrightarrow c}|=\sqrt{{{cos}^2}α+{{(2sinα-1)}^2}}$=$\sqrt{3{{sin}^2}α-4sinα+2}$;
令t=sinα,∵$α∈[0,\frac{π}{2}]$,∴t∈[0,1];
$|\overrightarrow{a}-\overrightarrow{c}|=\sqrt{3{t}^{2}-4t+2}$=$\sqrt{3(t-\frac{2}{3})^{2}+\frac{2}{3}}$;
∴$t=\frac{2}{3}$时,$|\overrightarrow{a}-\overrightarrow{c}|$取最小值$\frac{\sqrt{6}}{3}$,t=0时,$|\overrightarrow{a}-\overrightarrow{c}|$取最大值$\sqrt{2}$;
∴$|{\overrightarrow a-\overrightarrow c}|$的范围是$[\frac{\sqrt{6}}{3},\sqrt{2}]$.
点评 考查数量积的坐标运算,两角和的正余弦公式,以及向量坐标的减法运算,配方求二次函数最值的方法.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 0 | C. | 2 | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2+2\sqrt{2}$ | B. | $3+2\sqrt{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
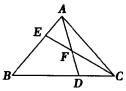 如图,在△ABC中,AE:EB=1:3,BD:DC=2:1,AD与CE相交于点F,则$\frac{EF}{FC}+\frac{AF}{FD}$的值为$\frac{3}{2}$.
如图,在△ABC中,AE:EB=1:3,BD:DC=2:1,AD与CE相交于点F,则$\frac{EF}{FC}+\frac{AF}{FD}$的值为$\frac{3}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com