Question

【题目】已知向量（其中），记，且满足.

（1）求函数的解析式；

（2）若关于的方程在上有三个不相等的实数根，求实数的取值范围。

Answer 1

【答案】(1) (2)

【解析】

（1）根据向量坐标运算公式，求出的表达式，化简为标准型，结合周期可得的解析式；

（2）结合所给区间，求出的值域，再利用根的分布问题求解.

（1）

由，得是函数的一个周期，

所以，的最小正周期，解得

又由已知，得 ,

因此，.

（2） 由，得

故：

因此函数的值域为.

设，

使关于的方程在上有三个不相等的实数根，当且仅当关于的方程在和上分别有一个实数根，或有一个实数根为1，另一实数根在区间上

令

①当关于的方程在和上分别有一个实数根时，

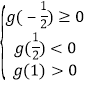解得

②当方程的一个根是时，，

另一个根为，不满足条件；

③当方程的一个根是时，，

另一个根为，不满足条件；

因此，满足条件的实数的取值范围是.