
【题目】已知函数![]() ,
, ![]() .
.
(1)若关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围;
的取值范围;
(2)设函数![]() ,若
,若![]() 在
在![]() 上存在极值,求
上存在极值,求![]() 的取值范围,并判断极值的正负.
的取值范围,并判断极值的正负.
【答案】(1) ![]() ;(2)答案见解析.
;(2)答案见解析.
【解析】试题分析:(1)由题意可知![]() 在
在![]() 上恒成立,构造新函数
上恒成立,构造新函数![]() ,
, ![]() ,求导根据函数的单调性及极值的判断,即可求得
,求导根据函数的单调性及极值的判断,即可求得![]() 在
在![]() 上单调递增,即可求得
上单调递增,即可求得![]() 的取值范围;
的取值范围;
(2)![]() 若
若![]() 在
在![]() 上存在极值,则
上存在极值,则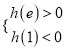 或
或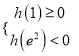 ,分类讨论,分别构造新函数,根据导数与函数的关系,即可求得
,分类讨论,分别构造新函数,根据导数与函数的关系,即可求得![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ)由![]() ,得
,得![]() .即
.即![]() 在
在![]() 上恒成立
上恒成立
设函数![]() ,
, ![]() .则
.则![]() .
.
设![]() .则
.则![]() .易知当
.易知当![]() 时,
时, ![]() .
.
∴![]() 在
在![]() 上单调递增,且
上单调递增,且![]() .即
.即![]() 对
对![]() 恒成立.
恒成立.
∴![]() 在
在![]() 上单调递增.
上单调递增.
∴当![]() 时,
时, ![]() .
.
∴![]() ,即
,即![]() 的取值范围是
的取值范围是![]() .
.
(Ⅱ)![]() ,
, ![]() .
.
∴![]()
![]() .
.
设![]() ,则
,则![]() .
.
由![]() ,得
,得![]() .
.
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
且![]() ,
, ![]() ,
, ![]() .
.
显然![]() .
.
结合函数图象可知,若![]() 在
在![]() 上存在极值,
上存在极值,
则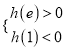 或
或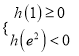 .
.
(ⅰ)当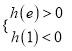 ,即
,即![]() 时,
时,
则必定![]() ,使得
,使得![]() ,且
,且![]() .
.
当![]() 变化时,
变化时, ![]() ,
, ![]() ,
, ![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
| - | 0 | + | 0 | - |
| - | 0 | + | 0 | - |
| ↘ | 极小值 | ↗ | 极大值 | ↘ |
∴当![]() 时,
时, ![]() 在
在![]() 上的极值为
上的极值为![]() ,且
,且![]() .
.
∵![]()
![]() .
.
设![]() ,其中
,其中![]() ,
, ![]() .
.
∵![]() ,∴
,∴![]() 在
在![]() 上单调递增,
上单调递增, ![]() ,当且仅当
,当且仅当![]() 时取等号.
时取等号.
∵![]() ,∴
,∴![]() .
.
∴当![]() 时,
时, ![]() 在
在![]() 上的极值
上的极值![]() .
.
(ⅱ)当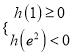 ,即
,即![]() 时,
时,
则必定![]() ,使得
,使得![]() .
.
易知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
此时, ![]() 在
在![]() 上的极大值是
上的极大值是![]() ,且
,且![]() .
.
∴当![]() 时,
时, ![]() 在
在![]() 上的极值为正数.
上的极值为正数.
综上所述:当![]() 时,
时, ![]() 在
在![]() 上存在极值,且极值都为正数.
上存在极值,且极值都为正数.
注:也可由![]() ,得
,得![]() .令
.令![]() 后再研究
后再研究![]() 在
在![]() 上的极值问题.
上的极值问题.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数, ![]() 为自然对数的底数),曲线
为自然对数的底数),曲线![]() 在与
在与![]() 轴的交点
轴的交点![]() 处的切线斜率为-1.
处的切线斜率为-1.
(1)求![]() 的值及函数
的值及函数![]() 的单调区间;
的单调区间;
(2)证明:当![]() 时,
时, ![]() ;
;
(3)证明:当![]() 时,
时, 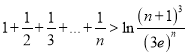 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地4个蔬菜大棚顶部,阳光照在一棵棵茁壮生长的蔬菜上,这些采用水培、无土栽培方式种植的各类蔬菜,成为该地区居民争相购买的对象,过去50周的资料显示,该地周光照量![]() (小时)都在30以上,其中不足50的周数大约5周,不低于50且不超过70的周数大约有35周,超过70的大约有10周,根据统计某种改良黄瓜每个蔬菜大棚增加量
(小时)都在30以上,其中不足50的周数大约5周,不低于50且不超过70的周数大约有35周,超过70的大约有10周,根据统计某种改良黄瓜每个蔬菜大棚增加量![]() (百斤)与每个蔬菜大棚使用农夫1号液体肥料
(百斤)与每个蔬菜大棚使用农夫1号液体肥料![]() (千克)之间对应数据为如图所示的折线图.
(千克)之间对应数据为如图所示的折线图.
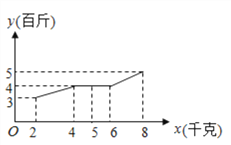
(1)依据数据的折线图,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;并根据所求线性回归方程,估计如果每个蔬菜大棚使用农夫1号肥料10千克,则这种改良黄瓜每个蔬菜大鹏增加量
;并根据所求线性回归方程,估计如果每个蔬菜大棚使用农夫1号肥料10千克,则这种改良黄瓜每个蔬菜大鹏增加量![]() 是多少斤?
是多少斤?
(2)因蔬菜大棚对光照要求较大,某光照控制仪商家为应对恶劣天气对光照的影响,为该基地提供了部分光照控制仪,该商家希望安装的光照控制仪尽可能运行,但每周光照控制仪最多可运行台数受周光照量![]() 限制,并有如下关系:
限制,并有如下关系:
周光照量 | 30<X<50 |
|
|
光照控制仪最多可运行台数 | 3 | 2 | 1 |
若某台光照控制仪运行,则该台光照仪周利润为4000元;若某台光照仪未运行,则该台光照仪周亏损500元,欲使商家周总利润的均值达到最大,应安装光照控制仪多少台?
附:回归方程系数公式: 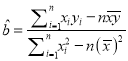 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
已知数列![]() 的前
的前![]() 项和
项和![]() ,且
,且![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)令![]() ,是否存在
,是否存在![]() ,使得
,使得![]() 、
、![]() 、
、![]() 成等比数列.若存在,求出所有符合条件的
成等比数列.若存在,求出所有符合条件的![]() 值;若不存在,请说明理由.
值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1}.
(1)若A∪B=A,求实数m的取值范围;
(2)当x∈Z时,求A的非空真子集的个数;
(3)当x∈R时,若A∩B=,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为打赢打好脱贫攻坚战,实现建档立卡贫困人员稳定增收,某地区把特色养殖确定为脱贫特色主导产业,助力乡村振兴.现计划建造一个室内面积为![]() 平方米的矩形温室大棚,并在温室大棚内建两个大小、形状完全相同的矩形养殖池,其中沿温室大棚前、后、左、右内墙各保留
平方米的矩形温室大棚,并在温室大棚内建两个大小、形状完全相同的矩形养殖池,其中沿温室大棚前、后、左、右内墙各保留![]() 米宽的通道,两养殖池之间保留2米宽的通道.设温室的一边长度为
米宽的通道,两养殖池之间保留2米宽的通道.设温室的一边长度为![]() 米,如图所示.
米,如图所示.

(1)将两个养殖池的总面积![]() 表示
表示![]() 为的函数,并写出定义域;
为的函数,并写出定义域;
(2)当温室的边长![]() 取何值时,总面积
取何值时,总面积![]() 最大?最大值是多少?
最大?最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com