
【题目】设函数![]() 为
为![]() 的导函数.
的导函数.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() 时,证明
时,证明![]() ;
;
(Ⅲ)设![]() 为函数
为函数![]() 在区间
在区间![]() 内的零点,其中
内的零点,其中![]() ,证明
,证明![]() .
.
【答案】(Ⅰ)单调递增区间为![]() 的单调递减区间为
的单调递减区间为![]() .(Ⅱ)见证明;(Ⅲ)见证明
.(Ⅱ)见证明;(Ⅲ)见证明
【解析】
(Ⅰ)由题意求得导函数的解析式,然后由导函数的符号即可确定函数![]() 的单调区间;
的单调区间;
(Ⅱ)构造函数![]() ,结合(Ⅰ)的结果和导函数的符号求解函数
,结合(Ⅰ)的结果和导函数的符号求解函数![]() 的最小值即可证得题中的结论;
的最小值即可证得题中的结论;
(Ⅲ)令![]() ,结合(Ⅰ),(Ⅱ)的结论、函数的单调性和零点的性质放缩不等式即可证得题中的结果.
,结合(Ⅰ),(Ⅱ)的结论、函数的单调性和零点的性质放缩不等式即可证得题中的结果.
(Ⅰ)由已知,有![]() .
.
当![]() 时,有
时,有![]() ,得
,得![]() ,则
,则![]() 单调递减;
单调递减;
当![]() 时,有
时,有![]() ,得
,得![]() ,则
,则![]() 单调递增.
单调递增.
所以,![]() 的单调递增区间为
的单调递增区间为![]() ,
,
![]() 的单调递减区间为
的单调递减区间为![]() .
.
(Ⅱ)记![]() .依题意及(Ⅰ)有:
.依题意及(Ⅰ)有:![]() ,
,
从而![]() .当
.当![]() 时,
时,![]() ,故
,故
![]() .
.
因此,![]() 在区间
在区间![]() 上单调递减,进而
上单调递减,进而![]() .
.
所以,当![]() 时,
时,![]() .
.
(Ⅲ)依题意,![]() ,即
,即![]() .
.
记![]() ,则
,则![]() .
.
且![]()
![]() .
.
由![]() 及(Ⅰ)得
及(Ⅰ)得![]() .
.
由(Ⅱ)知,当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上为减函数,
上为减函数,
因此![]() .
.
又由(Ⅱ)知![]() ,故:
,故:
![]()
![]() .
.
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,两个焦点与短轴一个顶点构成等腰直角三角形,过点
,两个焦点与短轴一个顶点构成等腰直角三角形,过点![]() 且与x轴不重合的直线l与椭圆交于M,N不同的两点.
且与x轴不重合的直线l与椭圆交于M,N不同的两点.
(Ⅰ)求椭圆P的方程;
(Ⅱ)当AM与MN垂直时,求AM的长;
(Ⅲ)若过点P且平行于AM的直线交直线![]() 于点Q,求证:直线NQ恒过定点.
于点Q,求证:直线NQ恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年
年![]() 月,电影《毒液》在中国上映,为了了解江西观众的满意度,某影院随机调查了本市观看影片的观众,现从调查人群中随机抽取部分观众.并用如图所示的表格记录了他们的满意度分数(
月,电影《毒液》在中国上映,为了了解江西观众的满意度,某影院随机调查了本市观看影片的观众,现从调查人群中随机抽取部分观众.并用如图所示的表格记录了他们的满意度分数(![]() 分制),若分数不低于
分制),若分数不低于![]() 分,则称该观众为“满意观众”,请根据下面尚未完成并有局部污损的频率分布表(如图所示),解决下列问题.
分,则称该观众为“满意观众”,请根据下面尚未完成并有局部污损的频率分布表(如图所示),解决下列问题.
组别 | 分组 | 频数 | 频率 |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
合计 |
|
|
(1)写出![]() 、
、![]() 的值;
的值;
(2)画出频率分布直方图,估算中位数;
(3)在选取的样本中,从满意观众中随机抽取![]() 名观众领取奖品,求所抽取的
名观众领取奖品,求所抽取的![]() 名观众中至少有
名观众中至少有![]() 名观众来自第
名观众来自第![]() 组的概率.
组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 如图,在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形,![]() 为等边三角形,平面
为等边三角形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,
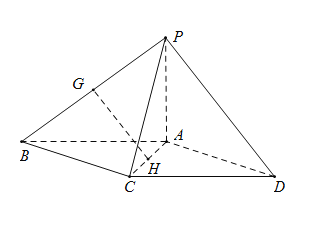
(Ⅰ)设![]() 分别为
分别为![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() 是双曲线
是双曲线![]() 的左,右焦点,点
的左,右焦点,点![]() 在双曲线上,且
在双曲线上,且![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
A. 若![]() ,则双曲线离心率的取值范围为
,则双曲线离心率的取值范围为![]()
B. 若![]() ,则双曲线离心率的取值范围为
,则双曲线离心率的取值范围为![]()
C. 若![]() ,则双曲线离心率的取值范围为
,则双曲线离心率的取值范围为![]()
D. 若![]() ,则双曲线离心率的取值范围为
,则双曲线离心率的取值范围为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,某企业每年消耗电费约24万元,为了节能减排,决定安装一个可使用15年的太阳能供电设备接入本企业电网,安装这种供电设备的工本费(单位:万元)与太阳能电池板的面积(单位:平方米)成正比,比例系数约为0.5.为了保证正常用电,安装后采用太阳能和电能互补供电的模式.假设在此模式下,安装后该企业每年消耗的电费![]() (单位:万元)与安装的这种太阳能电池板的面积
(单位:万元)与安装的这种太阳能电池板的面积![]() (单位:平方米)之间的函数关系是
(单位:平方米)之间的函数关系是![]() 为常数).记
为常数).记![]() 为该村安装这种太阳能供电设备的费用与该村15年共将消耗的电费之和.
为该村安装这种太阳能供电设备的费用与该村15年共将消耗的电费之和.
(1)试解释![]() 的实际意义,并建立
的实际意义,并建立![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 为多少平方米时,
为多少平方米时,![]() 取得最小值?最小值是多少万元?
取得最小值?最小值是多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com