【题目】已知函数f（x）=cos4x﹣sin4x．下列结论正确的是（ ）
A.函数f（x）在区间[0， 
]上是减函数
B.函数f（x）的图象关于原点对称
C.f（x）的最小正周期为
D.f（x）的值域为[﹣ 
， ]
备战中考寒假系列答案科目：高中数学 来源： 题型：
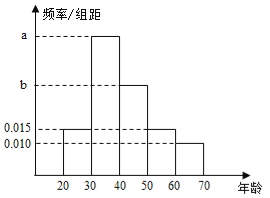
【题目】【广西南宁2017届高三检测】根据某电子商务平台的调查统计显示，参与调查的1000位上网购物者的年龄情况如图．
（1）已知
、
，
三个年龄段的上网购物者人数成等差数列，求
，
的值；
（2）该电子商务平台将年龄在
之间的人群定义为高消费人群，其他的年龄段定义为潜在消费人群，为了鼓励潜在消费人群的消费，该平台决定发放代金券，高消费人群每人发放50元的代金券，潜在消费人群每人发放80元的代金券，已经采用分层抽样的方式从参与调查的1000位上网购物者中抽取了10人，现在要在这10人中随机抽取3人进行回访，求此三人获得代金券总和
的分布列与数学期望．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知集合A={1，2，3}，集合B={x|a+1＜x＜6a﹣1}，其中a∈R．
（1）写出集合A的所有真子集；
（2）若A∩B={3}，求a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某钢厂打算租用
， 
两种型号的火车车皮运输900吨钢材， 
， 
两种车皮的载货量分别为36吨和60吨，租金分别为1.6万元/个和2.4万元/个，钢厂要求租车皮总数不超过21个，且
型车皮不多于
型车皮7个，分别用
， 
表示租用
， 
两种车皮的个数.
（Ⅰ）用
， 
列出满足条件的数学关系式，并画出相应的平面区域；
（Ⅱ）分别租用
， 
两种车皮的个数是多少时，才能使得租金最少？并求出此最小租金.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆C经过点
，且圆心
在直线
上，又直线
与圆C交于P,Q两点.
（1）求圆C的方程；
（2）若
，求实数
的值；
(3)过点
作直线
，且
交圆C于M,N两点，求四边形
的面积的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在矩形ABCD中，边AB、AD的长分别为2，1，若M，N分别是边BC、CD上的点，且满足 
= 
=λ．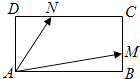 
（1）当λ= 
时，求向量 
和 
夹角的余弦值；
（2）求 
的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】据统计，某物流公司每天的业务中，从甲地到乙地的可配送的货物量
的频率分布直方图，如图所示，将频率视为概率，回答以下问题.
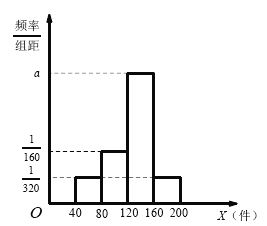
（1）求该物流公司每天从甲地到乙地平均可配送的货物量；
（2）该物流公司拟购置货车专门运营从甲地到乙地的货物，一辆货车每天只能运营一趟，每辆车每
趟最多只能装载40 件货物，满载发车，否则不发车。若发车，则每辆车每趟可获利1000 元；若未发车，
则每辆车每天平均亏损200 元。为使该物流公司此项业务的营业利润最大，该物流公司应该购置几辆货
车？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校从高一年级学生中随机抽取40名中学生，将他们的期中考试数学成绩（满分100分，成绩均为不低于40分的整数）分成六段： 
， 
，…， 
，得到如图所示的频率分布直方图.
（1）求图中实数
的值；
（2）若该校高一年级共有640人，试估计该校高一年级期中考试数学成绩不低于60分的人数；
（3）若从数学成绩在
与
两个分数段内的学生中随机选取2名学生，求这2名学生的数学成绩之差的绝对值不大于10的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
