
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为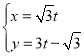 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的参数方程;
的参数方程;
(2)若![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
【题目】2013年华人数学家张益唐证明了孪生素数猜想的一个弱化形式,此事引起了国际数学界的轰动许多专家认为这是数论研究中的一项重大突破世界主流媒体都对这项重要成果作了报道并给予了高度评价,印度媒体甚至称赞张益唐为“中国的拉马努金”.孪生素数猜想是希尔伯特在1900年提出的23个问题之一,可以这样描述:存在无穷多个素数![]() ,使得
,使得![]() 是素数,素数对
是素数,素数对![]() 称为孪生素数.在不超过20的素数中,随机选取两个不同的数,其中能够组成孪生素数的概率是( )
称为孪生素数.在不超过20的素数中,随机选取两个不同的数,其中能够组成孪生素数的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】王老师在做折纸游戏,现有一张边长为1的正三角形纸片ABC,将点A翻折后恰好落在边BC上的点F处,折痕为DE,设![]() ,
,![]() .
.
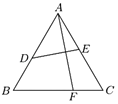
(1)求x、y满足的关系式;
(2)求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 分别是椭圆
分别是椭圆![]() 的上、下顶点,线段
的上、下顶点,线段![]() 长为
长为![]() ,椭圆的离心率为
,椭圆的离心率为![]() .
.
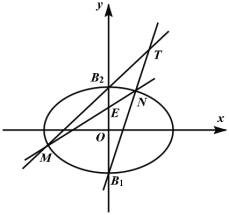
(1)求该椭圆的方程;
(2)已知过点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
①若直线![]() 的斜率为
的斜率为![]() ,求点
,求点![]() 的坐标;
的坐标;
②求证点![]() 在一条定直线上,并写出该直线方程.
在一条定直线上,并写出该直线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com