
给出下列四个命题:(1)若sin2A=sin2B,则△ABC是等腰三角形;(2)若sinA=cosB,则△ABC是直角三角形;(3)若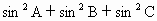 <2,则△ABC是钝三角形;(4)若cos(A-B)cos(B-C)cos(C-A)=1,则△ABC是直角三角形;以上命题正确的个数是
<2,则△ABC是钝三角形;(4)若cos(A-B)cos(B-C)cos(C-A)=1,则△ABC是直角三角形;以上命题正确的个数是
[ ]
|
本题考查三角形内三角关系的基础知识.在三角形内讨论三角问题,三内角有范围限制, A,B,C∈(0,π),若sin2A=sin2B,则2A=2B或2A=π-2B,故三角形为等腰三角形式直角三角形,故(1)错误,三角形内的三角函数问题,处理的方法与一般三角函数问题没有区别,因此讨论sinA=sinB,仍需统一三角函数名称,化正弦为余弦或化余弦为正弦,故sinA=sin( -B),故A= -B),故A= -B或A= -B或A= +B,三角形未必是直角三角形.讨论 +B,三角形未必是直角三角形.讨论 <2,需要降次,利用二倍角的余弦公式,cos2A+cos2B+cos2C+1>0,化简三角形内三角函数问题,注意隐含条件A+B+C=π的运用,利用和差化积公式可得cosAcosBcosC<0,可得三角形为钝角三角形.若cos(A-B)cos(B-C)cos(C-A)=1,注意三角函数值的范围,故cos(A-B)=cos(B-C)=cos(C-A)=1可得A=B=C,故三角形为正三角形. <2,需要降次,利用二倍角的余弦公式,cos2A+cos2B+cos2C+1>0,化简三角形内三角函数问题,注意隐含条件A+B+C=π的运用,利用和差化积公式可得cosAcosBcosC<0,可得三角形为钝角三角形.若cos(A-B)cos(B-C)cos(C-A)=1,注意三角函数值的范围,故cos(A-B)=cos(B-C)=cos(C-A)=1可得A=B=C,故三角形为正三角形. |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| y-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 12 |
| π |
| 12 |
| x |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2x-1 |
| (1+2x)2 |
| x•2x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com