
【题目】数列a1,a2……an是正整数1,2,……,n的任一排列,且同时满足以下两个条件:
①a1=1;②当n≥2时,|ai-ai+1|≤2(i=1,2,…,n-1).
记这样的数列个数为f(n).
(I)写出f(2),f(3),f(4)的值;
(II)证明f(2018)不能被4整除.
【答案】(Ⅰ)f(2)=1,f(3)=2,f(4)=4;(Ⅱ)见解析.
【解析】试题分析:(Ⅰ)根据题意,由f(n)的定义,计算即可得答案;
(Ⅱ)根据题意,把满足条件①②的数列称为n项的首项最小数列,对于n个数的首项最小数列,由于a1=1,故a2=2或3;分析可得递推关系为f(n)=f(n-1)+f(n-3)+1,进而求出f(2),f(3),…,f(2018)各数被4除的余数,分析可得它们构成14为周期的数列,即可得结论.
试题解析:
(Ⅰ)解:(Ⅰ)根据题意,①a1=1;②当n2时, |ai-ai+1|≤2(i=1,2,…,n1);
则f(2)=1,f(3)=2,f(4)=4.
(Ⅱ)证明:把满足条件①②的数列称为n项的首项最小数列.
对于n个数的首项最小数列,由于a1=1,故a2=2或3.
(1)若a2=2,则a2-1,a3-1,,an-1构成n-1项的首项最小数列,其个数为f(n-1);
(2)若a2=3,a3=2,则必有a4=4,故a4-3,a5-3,……,an-3构成n-3项的首项最小数列,其个数为f(n-3);
(3)若a2=3,则a3=4或a3=5.设ak+1是这数列中第一个出现的偶数,则前k项应该是1,3,,2k-1,ak+1是2k或2k-2,即ak与ak+1是相邻整数.
由条件②,这数列在ak+1后的各项要么都小于它,要么都大于它,因为2在ak+1之后,故ak+1后的各项都小于它.
这种情况的数列只有一个,即先排递增的奇数,后排递减的偶数.
综上,有递推关系:f(n)=f(n-1)+f(n-3)+1,n≥5.
由此递推关系和(I)可得,f(2),f(3),,f(2018)各数被4除的余数依次为:
1,1,2,0,2,1,2,1,3,2,0,0,3,0,1,1,2,0,…
它们构成14为周期的数列,又2018=14![]() 144+2,
144+2,
所以f(2018)被4除的余数与f(2)被4除的余数相同,都是1,
故f(2018)不能被4整除.


科目:高中数学 来源: 题型:
【题目】如图,在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北偏东30°,俯角为30°的B处,到11时10分又测得该船在岛北偏西60°,俯角为60°的C处.
(1)求船的航行速度是每小时多少千米?
(2)又经过一段时间后,船到达海岛的正西方向的D处,问此时船距岛A有多远?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的对称中心为原点O,焦点在x轴上,离心率为![]() ,且点
,且点![]() 在该椭圆上。
在该椭圆上。
(I)求椭圆C的方程;
(II)过椭圆C的左焦点![]() 的直线l与椭圆C相交于
的直线l与椭圆C相交于![]() 两点,若
两点,若![]() 的面积为
的面积为![]() ,求圆心在原点O且与直线l相切的圆的方程。
,求圆心在原点O且与直线l相切的圆的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假定下述数据是甲、乙两个供货商的交货天数:
甲:10 9 10 10 11 11 9 11 10 10
乙:8 10 14 7 10 11 10 8 15 12
估计两个供货商的交货情况,并问哪个供货商交货时间短一些,哪个供货商交货时间较具一致性与可靠性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,满足Sn=2an-1.(n∈N*)
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足bn=![]() an,求数列{bn}的前n项和Tn.
an,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1)五边形![]() 中,
中, ![]()
![]() ,将
,将![]() 沿
沿![]() 折到
折到![]() 的位置,得到四棱锥
的位置,得到四棱锥![]() ,如图(2),点
,如图(2),点![]() 为线段
为线段![]() 的中点,且
的中点,且![]() 平面
平面![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若直线![]() 与所成角的正切值为
与所成角的正切值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
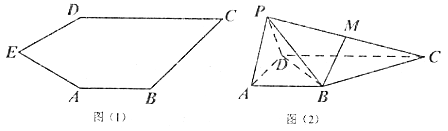
查看答案和解析>>
科目:高中数学 来源: 题型:
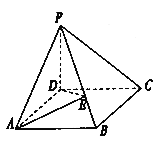
【题目】如图在棱锥![]() 中,
中, ![]() 为矩形,
为矩形, ![]() 面
面![]() ,
, ![]() ,
, ![]() 与面
与面![]() 成
成![]() 角,
角, ![]() 与面
与面![]() 成
成![]() 角.
角.
(1)在![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 面
面![]() ,若存在确定
,若存在确定![]() 点位置,若不存在,请说明理由;
点位置,若不存在,请说明理由;
(2)当![]() 为
为![]() 中点时,求二面角
中点时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB为圆O的直径,点E、F在圆O上,AB ∥EF,矩形ABCD所在平面与圆O所在的平面互相垂直.已知AB=2,EF=1.
(1)求证:平面DAF⊥平面CBF;
(2)求直线AB与平面CBF所成角的大小;
(3)求AD的长为何值时,平面DFC与平面FCB所成的锐二面角的大小为60°?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com