
【题目】关于不同的直线![]() 与不同的平面
与不同的平面![]() ,有下列六个命题:
,有下列六个命题:
①若![]() 则
则![]() ;
;
②若![]() 则
则![]() ;
;
③若![]() 且
且![]() 则
则![]() ;
;
④若![]() 且
且![]() 则
则![]() ;
;
⑤若![]() 且
且![]() 则
则![]() ;
;
⑥若![]() 且
且![]() 则
则![]() ;
;
其中正确命题的序号是__________;
【答案】①③⑤
【解析】
①:根据线面平行的性质定理、面面垂直的判定定理,结合平行线的性质进行判断即可;
②:根据线面平行的判定定理进行判断即可;
③:根据线面平行的性质定理、面面平行的性质,以及平行线的性质进行判断即可;
④:在正方体中可以找到特例进行判断即可;
⑤:根据平面法向量的性质和空间向量夹角公式进行判断即可;
⑥:根据面面平行的性质,结合直线与直线的位置关系进行判断即可.
①:因为![]() ,所以存在过直线
,所以存在过直线![]() 的一个平面与平面
的一个平面与平面![]() 交于直线
交于直线![]() ,显然有
,显然有![]() ,而
,而![]() ,所以
,所以![]() ,而
,而![]() ,因此
,因此![]() ,故本命题是真命题;
,故本命题是真命题;
②:只有当![]() ,
,![]() 才能推出
才能推出![]() ,故本命题是假命题;
,故本命题是假命题;
③:因为![]() ,所以存在过直线
,所以存在过直线![]() 的一个平面与平面
的一个平面与平面![]() 交于直线
交于直线![]() ,显然有
,显然有![]() ,又
,又![]() ,所以
,所以![]() ,因此
,因此![]() ,所以
,所以![]() ,故本命题是真命题;
,故本命题是真命题;
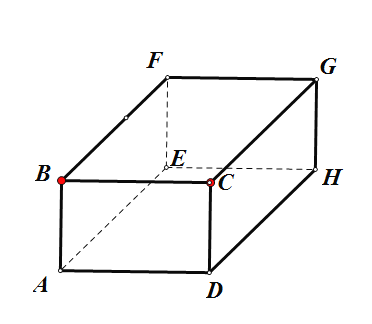
④:在如图的正方体![]() 中:
中:
平面![]() 记为平面
记为平面![]() ,平面
,平面![]() 记为平面
记为平面![]() ,直线
,直线![]() 记为直线
记为直线![]() ,直线
,直线![]() 记为直线
记为直线![]() ,显然符合
,显然符合![]()
![]() ,但是
,但是![]() ,(当然
,(当然![]() 也可以是异面直线),故本命题是假命题,
也可以是异面直线),故本命题是假命题,
⑤:因为![]() ,所以平面
,所以平面![]() 的法向量分别为:
的法向量分别为:![]() ,因为
,因为![]() 所以为
所以为![]() ,故本命题是真命题;
,故本命题是真命题;
⑥:因为![]() 且
且![]() 所以直线
所以直线![]() 没有交点,故两直线是平行线或异面直线,故本命题是假命题.
没有交点,故两直线是平行线或异面直线,故本命题是假命题.
故答案为:①③⑤


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】十九大提出,坚决打赢脱贫攻坚战,某帮扶单位为帮助定点扶贫村真脱贫,坚持扶贫同扶智相结合,帮助贫困村种植蜜柚,并利用电商进行销售,为了更好地销售,现从该村的蜜柚树上随机摘下了![]() 个蜜柚进行测重,其质量分别在
个蜜柚进行测重,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() (单位:克)中,其频率分布直方图如图所示,
(单位:克)中,其频率分布直方图如图所示,

(Ⅰ)已经按分层抽样的方法从质量落在![]() ,
,![]() 的蜜柚中抽取了
的蜜柚中抽取了![]() 个,现从这
个,现从这![]() 个蜜柚中随机抽取
个蜜柚中随机抽取![]() 个。求这
个。求这![]() 个蜜柚质量均小于
个蜜柚质量均小于![]() 克的概率:
克的概率:
(Ⅱ)以各组数据的中间值代表这组数据的平均水平,以频率代表概率,已知该贫困村的蜜柚树上大约还有![]() 个蜜柚等待出售,某电商提出了两种收购方案:
个蜜柚等待出售,某电商提出了两种收购方案:
方案一:所有蜜柚均以![]() 元/千克收购;
元/千克收购;
方案二:低于![]() 克的蜜柚以
克的蜜柚以![]() 元/个收购,高于或等于
元/个收购,高于或等于![]() 克的以
克的以![]() 元/个收购.
元/个收购.
请你通过计算为该村选择收益最好的方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一汽车厂生产![]() 三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表(单位:辆):
三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表(单位:辆):
轿车 | 轿车 | 轿车 | |
舒适型 | 100 | 150 |
|
标准型 | 300 | 450 | 600 |
按分层抽样的方法在这个月生产的轿车中抽取50辆,其中有![]() 类轿车10辆.
类轿车10辆.
(1)求![]() 的值;
的值;
(2)用随机抽样的方法从![]() 类舒适型轿车中抽取8辆,经检测它们的得分如下:4、8.6、9.2、9.6、8.7、9.3、9.0、8.2,把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
类舒适型轿车中抽取8辆,经检测它们的得分如下:4、8.6、9.2、9.6、8.7、9.3、9.0、8.2,把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆锥![]() (其中
(其中![]() 为顶点,
为顶点,![]() 为底面圆心)的侧面积与底面积的比是
为底面圆心)的侧面积与底面积的比是![]() ,则圆锥
,则圆锥![]() 与它的外接球(即顶点在球面上且底面圆周也在球面上)的体积比为__________.
与它的外接球(即顶点在球面上且底面圆周也在球面上)的体积比为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在单位正方体![]() 中,点
中,点![]() 在线段
在线段![]() 上运动,给出以下三个命题:
上运动,给出以下三个命题:
①三棱锥![]() 的体积为定值; ②二面角
的体积为定值; ②二面角![]() 的大小为定值;
的大小为定值;
③异面直线![]() 与直线
与直线![]() 所成的角为定值;
所成的角为定值;
其中真命题有( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:极坐标与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 是参数),以坐标原点
是参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若射线![]()
![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,与曲线
两点,与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 取最大值时
取最大值时![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】时值金秋十月,正是秋高气爽,阳光明媚的美好时刻。复兴中学一年一度的校运会正在密锣紧鼓地筹备中,同学们也在热切地期盼着,都想为校运会出一份力。小智同学则通过对学校有关部门的走访,随机地统计了过去许多年中的五个年份的校运会“参与”人数及相关数据,并进行分析,希望能为运动会组织者科学地安排提供参考。
附:①过去许多年来学校的学生数基本上稳定在3500人左右;②“参与”人数是指运动员和志愿者,其余同学均为“啦啦队员”,不计入其中;③用数字1、2、3、4、5表示小智同学统计的五个年份的年份数,今年的年份数是6;
统计表(一)
年份数x | 1 | 2 | 3 | 4 | 5 |
“参与”人数(y千人) | 1.9 | 2.3 | 2.0 | 2.5 | 2.8 |
统计表(二)
高一(3)(4)班参加羽毛球比赛的情况:
男生 | 女生 | 小计 | |
参加(人数) | 26 | b | 50 |
不参加(人数) | c | 20 | |
小计 | 44 | 100 |
(1)请你与小智同学一起根据统计表(一)所给的数据,求出“参与”人数y关于年份数x的线性回归方程![]() ,并预估今年的校运会的“参与”人数;
,并预估今年的校运会的“参与”人数;
(2)学校命名“参与”人数占总人数的百分之八十及以上的年份为“体育活跃年”.如果该校每届校运会的“参与”人数是互不影响的,且假定小智同学对今年校运会的“参与”人数的预估是正确的,并以这6个年份中的“体育活跃年”所占的比例作为任意一年是“体育活跃年”的概率。现从过去许多年中随机抽取9年来研究,记这9年中“体活跃年”的个数为随机变量![]() ,试求随机变量
,试求随机变量![]() 的分布列、期望
的分布列、期望![]() 和方差
和方差![]() ;
;
(3)根据统计表(二),请问:你能否有超过60%的把握认为“羽毛球运动”与“性别”有关?
参考公式和数据一: ,
,![]() ,
,![]() ,
,![]()
参考公式二: ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线![]() :
:![]() ,(
,(![]() 为参数),将曲线
为参数),将曲线![]() 上的所有点的横坐标缩短为原来的
上的所有点的横坐标缩短为原来的![]() ,纵坐标缩短为原来的
,纵坐标缩短为原来的![]() 后得到曲线
后得到曲线![]() ,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为 。
。
(1)求曲线![]() 的极坐标方程和直线l的直角坐标方程;
的极坐标方程和直线l的直角坐标方程;
(2)设直线l与曲线![]() 交于不同的两点A,B,点M为抛物线
交于不同的两点A,B,点M为抛物线![]() 的焦点,求
的焦点,求![]() 的值。
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com