
【题目】2019年4月20日,福建省人民政府公布了“3+1+2”新高考方案,方案中“2”指的是在思想政治、地理、化学、生物4门中选择2门.“2”中记入高考总分的单科成绩是由原始分转化得到的等级分,学科高考原始分在全省的排名越靠前,等级分越高小明同学是2018级的高一学生.已确定了必选地理且不选政治,为确定另选一科,小明收集并整理了化学与生物近10大联考的成绩百分比排名数据x(如x=19的含义是指在该次考试中,成绩高于小明的考生占参加该次考试的考生数的19%)绘制茎叶图如下.

(1)分别计算化学、生物两个学科10次联考的百分比排名的平均数;中位数;
(2)根据已学的统计知识,并结合上面的数据,帮助小明作出选择.并说明理由.
科目:高中数学 来源: 题型:
【题目】现从某医院中随机抽取了七位医护人员的关爱患者考核分数(患者考核:10分制),用相关的特征量![]() 表示;医护专业知识考核分数(试卷考试:100分制),用相关的特征量
表示;医护专业知识考核分数(试卷考试:100分制),用相关的特征量![]() 表示,数据如下表:
表示,数据如下表:
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程(计算结果精确到0.01);
的线性回归方程(计算结果精确到0.01);
(Ⅱ)利用(I)中的线性回归方程,分析医护专业考核分数的变化对关爱患者考核分数的影响,并估计某医护人员的医护专业知识考核分数为95分时,他的关爱患者考核分数(精确到0.1);

(Ⅲ)现要从医护专业知识考核分数95分以下的医护人员中选派2人参加组建的“九寨沟灾后医护小分队”培训,求这两人中至少有一人考核分数在90分以下的概率.
附:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为
查看答案和解析>>
科目:高中数学 来源: 题型:
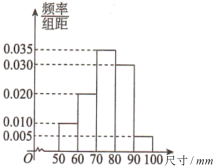
【题目】某工厂为检验车间一生产线工作是否正常,现从生产线中随机抽取一批零件样本,测量它们的尺寸(单位:![]() )并绘成频率分布直方图,如图所示.根据长期生产经验,可以认为这条生产线正常状态下生产的零件尺寸
)并绘成频率分布直方图,如图所示.根据长期生产经验,可以认为这条生产线正常状态下生产的零件尺寸![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为零件样本平均数
近似为零件样本平均数![]() ,
,![]() 近似为零件样本方差
近似为零件样本方差![]() .
.
(1)求这批零件样本的![]() 和
和![]() 的值(同一组中的数据用该组区间的中点值作代表);
的值(同一组中的数据用该组区间的中点值作代表);
(2)假设生产状态正常,求![]() ;
;
(3)若从生产线中任取一零件,测量其尺寸为![]() ,根据
,根据![]() 原则判断该生产线是否正常?
原则判断该生产线是否正常?
附:![]() ;若
;若![]() ,则
,则![]() ,
, ![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】手机支付也称为移动支付![]() ,是指允许移动用户使用其移动终端(通常是手机)对所消费的商品或服务进行账务支付的一种服务方式.继卡类支付、网络支付后,手机支付俨然成为新宠.某金融机构为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有100个人,把这100个人按照年龄分成5组,然后绘制成如图所示的频率分布表和频率分布直方图.
,是指允许移动用户使用其移动终端(通常是手机)对所消费的商品或服务进行账务支付的一种服务方式.继卡类支付、网络支付后,手机支付俨然成为新宠.某金融机构为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有100个人,把这100个人按照年龄分成5组,然后绘制成如图所示的频率分布表和频率分布直方图.
组数 | 第l组 | 第2组 | 第3组 | 第4组 | 第5组 |
分组 |
|
|
|
|
|
频数 | 20 | 36 | 30 | 10 | 4 |

(1)求![]() ;
;
(2)从第l,3,4组中用分层抽样的方法抽取6人,求第l,3,4组抽取的人数:
(3)在(2)抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]() .
.

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年春季,世界各地相继出现流感疫情,这已经成为全球性的公共卫生问题.为了考察某种流感疫苗的效果,某实验室随机抽取100只健康小鼠进行试验,得到如下列联表:
感染 | 未感染 | 总计 | |
注射 | 10 | 40 | 50 |
未注射 | 20 | 30 | 50 |
总计 | 30 | 70 | 100 |
参照附表,在犯错误的概率最多不超过__________的前提下,可认为“注射疫苗”与“感染流感”有关系.
(参考公式:![]() .)
.)
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com