
(2)写出函数y=|x|的单调区间及其图像的对称轴,观察:在函数图像对称轴两侧的单调性有什么特点?
(3)定义在[-4,8]上的函数y=f(x)的图像关于直线x=2对称,y=f(x)的部分图像如图所示,请补全函数y=f(x)的图像,并写出其单调区间,观察:在函数图像对称轴两侧的单调性有什么特点?

(4)由以上你发现了什么结论?试加以证明.
思路分析:本题探讨函数的单调性的性质.利用归纳、猜想、证明的方法得到结论,用定义证明结论.
解:(1)函数y=x2-2x的单调递减区间是(-∞,1),单调递增区间是(1,+∞);对称轴是直线x=1;区间(-∞,1)和区间(1,+∞)关于直线x=1对称,单调性相反.
(2)函数y=|x|的单调递减区间是(-∞,0),单调递增区间是(0,+∞);对称轴是y轴即直线x=0;区间(-∞,0)和区间(0,+∞)关于直线x=0对称,单调性相反.
(3)函数y=f(x),x∈[-4,8]的图像如图所示.

函数y=f(x)的单调递增区间是[-4,-1],[2,5];单调递减区间是[5,8],[-1,2];区间[-4,-1]和区间[5,8]关于直线x=2对称,单调性相反,区间[-1,2]和区间[2,5]关于直线x=2对称,单调性相反.
(4)可以发现结论:如果函数y=f(x)的图像关于直线x=m对称,那么函数y=f(x)在直线x=m两侧对称单调区间内具有相反的单调性.证明如下:
不妨设函数y=f(x)在对称轴直线x=m的右侧一个区间[a,b]上是增函数,区间[a,b]关于直线x=m的对称区间是[2m-b,2m-a].
由于函数y=f(x)的图像关于直线x=m对称,则f(x)=f(2m-x).
设2m-b≤x1<x2≤2m-a,则b≥2m-x1>2m-x2≥a,
f(x1)-f(x2)=f(2m-x1)-f(2m-x2).
又∵函数y=f(x)在[a,b]上是增函数,∴f(2m-x1)-f(2m-x2)>0.
∴f(x1)-f(x2)>0.
∴f(x1)>f(x2).
∴函数y=f(x)在区间[2m-b,2m-a]上是减函数.
∴当函数y=f(x)在对称轴直线x=m的右侧一个区间[a,b]上是增函数时,在[a,b]关于直线x=m的对称区间[2m-b,2m-a]上则是减函数,即单调性相反.
因此有结论:如果函数y=f(x)的图像关于直线x=m对称,那么函数y=f(x)在对称轴两侧的对称单调区间内具有相反的单调性.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
(1)写出函数f(x)的解析式;
(2)证明:函数f(x)的图象关于直线y=x?对称;
(3)当x∈M时,函数f(x)的最大值为2+m2,最小值为2-![]() ,试确定集合M.
,试确定集合M.
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数f(x)=loga(x-3a)(a>0且a≠1),当点P(x,y)是函数y=f(x)图像上的点时,点Q(x-2a,-y)是函数y=g(x)图像上的点.
(1)写出函数y=g(x)的解析式;
(2)若当x∈[a+2,a+3]时,恒有|f(x)-g(x)|≤1,试确定a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011年山西省忻州市高一上学期联考数学试卷A 题型:解答题
(本题满分12分)
阅读右图的流程图.
(1)写出函数y = f (x)的解析式;
(2)由(1)中的函数y = f (x)表示的曲线与直线y =1围成的三角
形的内切圆记为圆O,若向这个三角形内投掷一个点,求这
个点落入圆O内的概率.

查看答案和解析>>
科目:高中数学 来源:2010年重庆市高一上学期期中考试数学试题 题型:解答题
(本小题满分10分)
已知函数 ,当点 (x,y)
是函数y = f (x) 图象上的点时,点
,当点 (x,y)
是函数y = f (x) 图象上的点时,点 是函数y =
g(x) 图象上的点.
是函数y =
g(x) 图象上的点.
(1) 写出函数y = g (x) 的表达式;
(2)
当g(x)-f (x)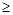 0时,求x的取值范围;
0时,求x的取值范围;
(3)
当x在 (2) 所给范围内取值时,求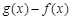 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com