
【题目】已知![]() 是定义在R上的偶函数且以2为周期,则“
是定义在R上的偶函数且以2为周期,则“![]() 为
为![]() 上的增函数”是“
上的增函数”是“![]() 为
为![]() 上的减函数”的
上的减函数”的![]()
![]()
A. 充分而不必要的条件B. 必要而不充分的条件
C. 充要条件D. 既不充分也不必要的条件
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的离心率为
)的离心率为![]() ,椭圆
,椭圆![]() 与
与![]() 轴交于
轴交于![]() 两点,且
两点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 是椭圆
是椭圆![]() 上的一个动点,且点
上的一个动点,且点![]() 在
在![]() 轴的右侧,直线
轴的右侧,直线![]() 与直线
与直线![]() 交于
交于![]() 两点,若以
两点,若以![]() 为直径的圆与
为直径的圆与![]() 轴交于
轴交于![]() ,求点
,求点![]() 横坐标的取值范围及
横坐标的取值范围及![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲袋中装有3个白球和5个黑球,乙袋中装有4个白球和6个黑球,现从甲袋中随机取出一个球放入乙袋中,充分混合后,再从乙袋中随机取出一个球放回甲袋中,则甲袋中白球没有减少的概率为____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】火把节是彝族、白族、纳西族、基诺族、拉祜族等民族的古老传统节日,有着深厚的民俗文化内涵,被称为“东方的狂欢节”凉山州旅游局为了解民众对火把节知识的知晓情况,对西昌市区 A,B 两小区的部分居民开展了问卷调查,他们得分(满分100分)数据,统计结果如下:
A小区 | ||||
得分范围/分 |
|
|
|
|
频率 |
|
|
|
|
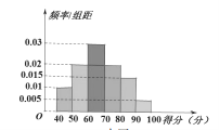
B小区
(1)以每组数据的中点值作为该组数据的代表,求B小区的平均分;
(2)若A小区得分在![]() 内的人数为
内的人数为![]() 人,B小区得分在
人,B小区得分在![]() 内的人数为
内的人数为![]() 人,求在 A,B 两小区中所有参加问卷调查的居民中得分不低于
人,求在 A,B 两小区中所有参加问卷调查的居民中得分不低于![]() 分的频率;
分的频率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 长轴的两顶点为
长轴的两顶点为![]() 、
、![]() ,左、右焦点分别为
,左、右焦点分别为![]() 、
、![]() ,焦距为
,焦距为![]() ,且
,且![]() ,过
,过![]() 且垂直于
且垂直于![]() 轴的直线被椭圆
轴的直线被椭圆![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)在双曲线![]() 上取点
上取点![]() 异于顶点,直线
异于顶点,直线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,若直线
,若直线![]() 、
、![]() 、
、![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() 、
、![]() 、
、![]() ,试证明:
,试证明:![]() 为定值;
为定值;
(3)在椭圆![]() 外的抛物线
外的抛物线![]() 上取一点
上取一点![]() ,若
,若![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定椭圆 C : ![]()
![]() ,称圆心在原点,半径为
,称圆心在原点,半径为![]() 的圆是椭圆 C 的“伴随圆”.若椭圆 C 的一个焦点为 F1(
的圆是椭圆 C 的“伴随圆”.若椭圆 C 的一个焦点为 F1(![]() , 0) ,其短轴上的一个端点到 F1 的距离为
, 0) ,其短轴上的一个端点到 F1 的距离为![]()
(1)求椭圆 C 的方程及其“伴随圆”方程;
(2)若倾斜角 45°的直线 l 与椭圆 C 只有一个公共点,且与椭圆 C 的伴随圆相交于 M .N 两点,求弦 MN 的的长;
(3)点 P 是椭圆 C 的伴随圆上一个动点,过点 P 作直线 l1、l2,使得 l1、l2与椭圆 C 都只有一个公共点,判断l1、l2的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com