
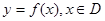 ,若存在常数
,若存在常数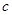 ,对任意
,对任意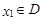 ,存在唯一
,存在唯一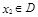 的,使得
的,使得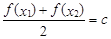 ,则称函数
,则称函数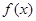 在
在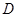 上的均值为
上的均值为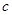 ,已知
,已知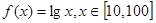 ,则函数
,则函数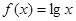 在
在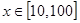 上的均值为。( )
上的均值为。( )A. | B. | C. | D. |
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
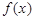 满足在集合
满足在集合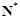 上的值域仍是集合
上的值域仍是集合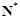 ,则把函数
,则把函数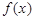 称为N函数.
称为N函数.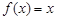 就是N函数.
就是N函数.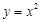 ,②
,②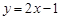 ,③
,③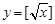 中,哪些是N函数?(只需写出判断结果);
中,哪些是N函数?(只需写出判断结果);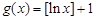 是否为N函数,并证明你的结论;
是否为N函数,并证明你的结论;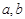 ,函数
,函数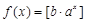 都不是N函数.
都不是N函数.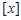 ”表示不超过
”表示不超过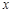 的最大整数)
的最大整数)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (单位:米)与生长年限t(单位:年)
(单位:米)与生长年限t(单位:年) .(设该生物出生时t=0)
.(设该生物出生时t=0) 年,该生物长得最快,求
年,该生物长得最快,求 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 元.公司拟投入
元.公司拟投入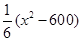 万元作为技改费用,投入50万元作为固定宣传费用,投入
万元作为技改费用,投入50万元作为固定宣传费用,投入 万元作为浮动宣传费用.试问:当该商品明年的销售量
万元作为浮动宣传费用.试问:当该商品明年的销售量 至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 的一个近似解时,现在已经将一根锁定在(1,2)内,则下一步可断定该根所在的区间为( )
的一个近似解时,现在已经将一根锁定在(1,2)内,则下一步可断定该根所在的区间为( )| A.(1.4,2) | B.(1,1.4) | C.(1,1.5) | D.(1.5,2) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 )x-
)x- . 其中
. 其中 ,t为常数;集合M={x
,t为常数;集合M={x ﹤0,
﹤0, },则对任意实常数t,总有
},则对任意实常数t,总有A.-3 M,0 M,0 M M | B.-3 M,0 M,0 M M |
C.-3 M,0 M,0 M M | D.-3 M,0 M,0 M M |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com