
【题目】已知函数f(x)=a(x﹣1)2+lnx+1,g(x)=f(x)﹣x,其中a∈R.
(Ⅰ)当a=﹣ ![]() 时,求函数f(x)的极值;
时,求函数f(x)的极值;
(Ⅱ)当a>0时,求函数g(x)的单调区间;
(Ⅲ)当x∈[1,+∞)时,若y=f(x)图象上的点都在 ![]() 所表示的平面区域内,求实数a的取值范围.
所表示的平面区域内,求实数a的取值范围.
【答案】解:(Ⅰ)当a=﹣ ![]() 时,f(x)=﹣
时,f(x)=﹣ ![]() x2+
x2+ ![]() x+lnx+
x+lnx+ ![]() ,
,
f(x)的定义域为(0,+∞),f′(x)=﹣ ![]() ;
;
列表讨论f′(x)和f(x)的变化情况:
x | (0,2) | 2 | (2,+∞) |
f′(x) | + | 0 | ﹣ |
f(x) | ↗ | 极大值 | ↘ |
∴当x=2时,f(x)取得极大值f(2)=ln2+ ![]() ;
;
(Ⅱ)当a>0时,g(x)=ax2﹣(2a+1)x+lnx+a+1,
g(x)的定义域为(0,+∞),
g′(x)= 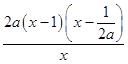 ,
,
令g′(x)=0,得x=1或x= ![]() ,
,
①当0<a< ![]() ,即
,即 ![]() >1时,
>1时,
由g′(x)<0,解得:1<x< ![]() ,
,
由g′(x)>0,解得:0<x<1或x> ![]() ,
,
∴g(x)在(1, ![]() )上单调递减,
)上单调递减,
在(0,1),( ![]() ,+∞)上单调递增;
,+∞)上单调递增;
②当a= ![]() ,即
,即 ![]() =1时,在(0,+∞)上,g′(x)≥0,
=1时,在(0,+∞)上,g′(x)≥0,
∴g(x)在(0,+∞)上单调递增;
③当a> ![]() ,即0<
,即0< ![]() <1时,
<1时,
由g′(x)<0,解得 ![]() <x<1,由g′(x)>0,解得0<x<
<x<1,由g′(x)>0,解得0<x< ![]() 或x>1,
或x>1,
∴g(x)在( ![]() ,1)上单调递减,
,1)上单调递减,
在(0, ![]() ),(1,+∞)上单调递增.
),(1,+∞)上单调递增.
(Ⅲ)∵y=f(x)图象上的点都在 ![]() 所表示的平面区域内,
所表示的平面区域内,
∴当x∈[1,+∞)时,f(x)﹣x≤0恒成立,
即当x∈[1,+∞)时,g(x)=a(x﹣1)2+lnx+1﹣x≤0恒成立.
只需g(x)max≤0;
①当a>0时,由(Ⅱ)知,
当0<a< ![]() 时,g(x)在(1,
时,g(x)在(1, ![]() )上单调递减,在(
)上单调递减,在( ![]() ,+∞)上单调递增,
,+∞)上单调递增,
∴g(x)在[1,+∞)上无最大值,不满足条件;
当a≥ ![]() 时,g(x) 在(1,+∞)上单调递增,
时,g(x) 在(1,+∞)上单调递增,
∴g(x)在[1,+∞)上无最大值,不满足条件;
②当a=0时,g′(x)=﹣ ![]() ,在(1,+∞)上,g′(x)<0,
,在(1,+∞)上,g′(x)<0,
∴g(x)在[1,+∞)上单调递减,g(x)≤g(1)=0成立;
③当a<0时,g′(x)= 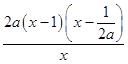 ,在(1,+∞)上,g′(x)<0,
,在(1,+∞)上,g′(x)<0,
∴g(x)在[1,+∞)上单调递减,g(x)≤g(1)=0成立,
综上可知,实数a的取值范围是a≤0
【解析】(Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极大值即可;(Ⅱ)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;(Ⅲ)问题转化为x∈[1,+∞)时,g(x)=a(x﹣1)2+lnx+1﹣x≤0恒成立,只需g(x)max≤0即可,根据函数的单调性求出a的范围.
【考点精析】利用利用导数研究函数的单调性和函数的极值与导数对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥S—ABCD的底面是正方形,侧棱SA⊥底面ABCD,
过A作AE垂直SB交SB于E点,作AH垂直SD交SD于H点,平面AEH交SC于K点,且AB=1,SA=2.

(1)证明E、H在以AK为直径的圆上,且当点P是SA上任一点时,试求![]() 的最小值;
的最小值;
(2)求平面AEKH与平面ABCD所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),圆
为参数),圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),圆
为参数),圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).若直线
为参数).若直线![]() 分别与圆
分别与圆![]() 和圆
和圆![]() 交于不同于原点的点
交于不同于原点的点![]() 和
和![]() .
.
(1)以直角坐标系的原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,求圆
轴的正半轴为极轴,建立极坐标系,求圆![]() 和圆
和圆![]() 的极坐标方程;
的极坐标方程;
(2)求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,⊙O是以AB为直径的圆,点C在圆上,在△ABC和△ACD中,∠ADC=90°,∠BAC=∠CAD,DC的延长线与AB的延长线交于点E.若EB=6,EC=6 ![]() ,则BC的长为 .
,则BC的长为 . 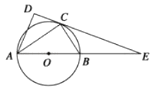
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C: ![]() =1(a>b>0)的中心在原点,焦点在x轴上,焦距为2,且与椭圆x2+
=1(a>b>0)的中心在原点,焦点在x轴上,焦距为2,且与椭圆x2+ ![]() =1有相同离心率,直线l:y=kx+m与椭圆C交于不同的A,B两点.
=1有相同离心率,直线l:y=kx+m与椭圆C交于不同的A,B两点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若在椭圆C上存在点Q,满足 ![]() ,(O为坐标原点),求实数λ取值范围.
,(O为坐标原点),求实数λ取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某测试中,卷面满分为100分,60分为及格,为了调查午休对本次测试前两个月复习效果的影响,特对复习中进行午休和不进行午休的考生进行了测试成绩的统计,数据如下表所示:
分数段 | 29~ 40 | 41~ 50 | 51~ 60 | 61~ 70 | 71~ 80 | 81~ 90 | 91~ 100 |
午休考 生人数 | 23 | 47 | 30 | 21 | 14 | 31 | 14 |
不午休 考生人数 | 17 | 51 | 67 | 15 | 30 | 17 | 3 |
(1)根据上述表格完成列联表:
及格人数 | 不及格人数 | 总计 | |
午休 | |||
不午休 | |||
总计 |
(2)根据列联表可以得出什么样的结论?对今后的复习有什么指导意义?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,AB、BC、BD两两垂直,AB=BC=BD=4,E、F分别为棱BC、AD的中点. 
(1)求异面直线AB与EF所成角的余弦值;
(2)求E到平面ACD的距离;
(3)求EF与平面ACD所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com