
【题目】如图,在△ABC中,∠BAC=120°,AC=3,△ABC的面积等于 ![]() ,D为边长BC上一点.
,D为边长BC上一点. 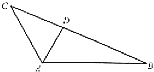
(1)求BC的长;
(2)当AD= ![]() 时,求cos∠CAD的值.
时,求cos∠CAD的值.
【答案】
(1)解:在△ABC中,∠BAC=120°,AC=3,△ABC的面积等于 ![]() ACABsin∠BAC=
ACABsin∠BAC= ![]() 3AB
3AB ![]() =
= ![]() ,
,
∴AB=5,再由余弦定理可得BC2=AB2+AC2﹣2ABACcos∠BAC=25+9﹣2×5×3×(﹣ ![]() )=49,
)=49,
∴BC=7.
(2)解:由题意可得cosC= ![]() =
= ![]() ,sinC=
,sinC= ![]() .
.
D为边长BC上一点,当AD= ![]() 时,△ACD中,利用正弦定理可得
时,△ACD中,利用正弦定理可得 ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
求得sin∠ADC= ![]() ,∴cos∠ADC=±
,∴cos∠ADC=± ![]() =±
=± ![]() .
.
当 cos∠ADC= ![]() ,cos∠CAD=﹣cos(C+∠ADC)=﹣cosCcos∠ADC+sinCsin∠ADC
,cos∠CAD=﹣cos(C+∠ADC)=﹣cosCcos∠ADC+sinCsin∠ADC
=﹣ ![]()
![]() +
+ ![]()
![]() =
= ![]() .
.
当 cos∠ADC=﹣ ![]() ,cos∠CAD=﹣cos(C+∠ADC)=﹣cosCcos∠ADC+sinCsin∠ADC
,cos∠CAD=﹣cos(C+∠ADC)=﹣cosCcos∠ADC+sinCsin∠ADC
=﹣ ![]() (﹣
(﹣ ![]() )+
)+ ![]()
![]() =
= ![]()
【解析】(1)由条件利用余弦定理、三角形的面积公式先求得AB的值,可得BC的值.(2)利用正弦定理求得sin∠ADC 的值,可得cos∠ADC 的值,再利用两角和的余弦公式,求得cos∠CAD=﹣cos(C+∠ADC)的值.
【考点精析】本题主要考查了余弦定理的定义的相关知识点,需要掌握余弦定理:![]() ;
;![]() ;
;![]() 才能正确解答此题.
才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x﹣ ![]() 存在单调递减区间,且y=f(x)的图象在x=0处的切线l与曲线y=ex相切,符合情况的切线l( )
存在单调递减区间,且y=f(x)的图象在x=0处的切线l与曲线y=ex相切,符合情况的切线l( )
A.有3条
B.有2条
C.有1条
D.不存在
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017四川资阳4月模拟】共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),…,[90,100] 分成5组,制成如图所示频率分直方图.
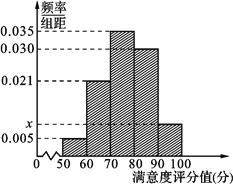
(Ⅰ) 求图中![]() 的值;
的值;
(Ⅱ) 已知满意度评分值在[90,100]内的男生数与女生数的比为2:1,若在满意度评分值为[90,100]的人中随机抽取4人进行座谈,设其中的女生人数为随机变量X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上![]() 件产品作为样本称出它们的重量(单位:克),重量的分组区间为
件产品作为样本称出它们的重量(单位:克),重量的分组区间为![]() ,
,![]() , ,
, ,![]() ,由此得到样本的频率分布直方图,如图所示.
,由此得到样本的频率分布直方图,如图所示.
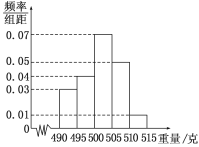
(1)根据频率分布直方图,求重量超过![]() 克的产品数量;
克的产品数量;
(2)在上述抽取的![]() 件产品中任取
件产品中任取![]() 件,设
件,设![]() 为重量超过
为重量超过![]() 克的产品数量,求
克的产品数量,求![]() 的分布列;
的分布列;
(3)从该流水线上任取![]() 件产品,求恰有
件产品,求恰有![]() 件产品的重量超过
件产品的重量超过![]() 克的概率.
克的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记集合A={(x,y)|x2+y2≤16}和集合B={(x,y)|x+y﹣4≤0,x≥0,y≥0}表示的平面区域分别为Ω1 , Ω2 , 若在区域Ω1内任取一点M(x,y),则点M落在区域Ω2的概率为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}满足a1+3a2+32a3+…+3n﹣1an= ![]() ,n∈N* .
,n∈N* .
(1)求数列{an}的通项;
(2)设 ![]() ,求数列{bn}的前n项和Sn .
,求数列{bn}的前n项和Sn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com