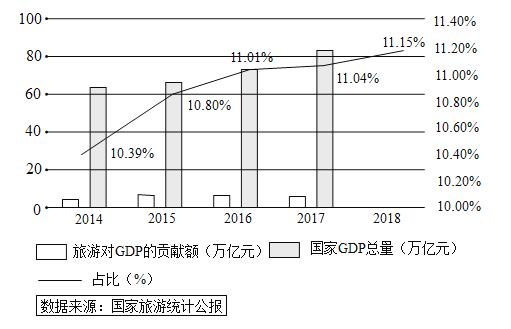
【题目】当前，旅游已经成为新时期人民群众美好生活和精神文化需求的重要内容.旅游是综合性产业，是拉动经济发展的重要动力，也为整个经济结构调整注入活力.文化旅游产业研究院发布了《2019年中国文旅产业发展趋势报告》，报告指出：旅游业稳步增长，每年占国家GDP总量的比例逐年增加，如图及下表为2014年到2018年的相关统计数据.
旅游收入占国家GDP总量比例趋势 | |||||
年份： | 1 | 2 | 3 | 4 | 5 |
占比： | 10.4 | 10.8 | 11.0 | 11.0 | 11.2 |
（1）根据以上数据，求出占比
关于年份
的线性回归方程
；
（2）根据（1）所求线性回归方程，预测2019年的旅游收入所占的比例.
附：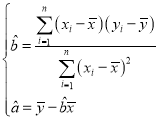
.
快乐小博士巩固与提高系列答案科目：高中数学 来源： 题型：
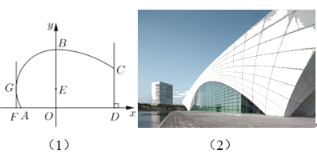
【题目】图（1）为东方体育中心，其设计方案侧面的外轮廓线如图（2）所示；曲线
是以点
为圆心的圆的一部分，其中
，曲线
是抛物线
的一部分；
且
恰好等于圆的半径，
与圆相切且
.
（1）若要求
米，
米，求
与
的值；
（2）当
时，若要求
不超过45米，求的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆的中心在原点，焦点在x轴上
分别为左、右焦点，椭圆的一个顶点与两焦点构成等边三角形，且
．
（1）求椭圆方程；
（2）对于x轴上的某一点T，过T作不与坐标轴平行的直线L交椭圆于
两点，若存在x轴上的点S，使得对符合条件的L恒有
成立，我们称S为T的一个配对点，当T为左焦点时，求T的配对点的坐标；
（3）在（2）条件下讨论当T在何处时，存在有配对点？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆C的一个顶点为
，焦点在x轴上，若右焦点到直线
的距离为3．
Ⅰ
求椭圆C的方程；
Ⅱ设椭圆C与直线
相交于不同的两点M，N，线段MN的中点为E．
当
时，射线OE交直线
于点
为坐标原点，求
的最小值；
当
，且
时，求m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某中学随机抽取部分高一学生调査其每日自主安排学习的时间（单位：分钟），并将所得数据绘制成如图所示的频率分布直方图，其中自主安排学习时间的范围是[0，100]，样本数据分组为[0，20），[20，40），[40，60），[60，80），[80，100].
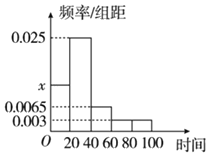
（1）求直方图中x的值；
（2）现采用分层抽样的方式从每日自主安排学习时间不超过40分钟的学生中随机抽取6人，若从这6人中随机抽取2人进行详细的每日时间安排调查，求抽到的2人每日自主安排学习时间均不低于20分钟的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的右焦点与短轴两端点构成一个面积为2的等腰直角三角形，
为坐标原点．
（1）求椭圆
的方程；
（2）设点
在椭圆上，点
在直线
上，且
，求证：
为定值；
（3）设点
在椭圆上运动，
，且点到直线
的距离为常数
，求动点
的轨迹方程．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
