
����Ŀ������Ҫ���ij��ҵ������ij��Ʒ�ƵĴ�װţ�̵������Ƿ��꣬�ִ�700��ţ���г�ȡ50�����м��飮�������������ȡ����ʱ���Ƚ�700��ţ�̰�001��002������700���б�ţ���������������3�е�1������ʼ���Ҷ������ȶ�����5��ţ�̵ı����614��593��379��242��203�������Դ˷�ʽ�������Ҷ�������������3��ţ�̵ı���� �� ������ժȡ�����������1������5�У� 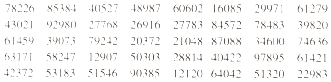
���𰸡�104��088��346
���������⣺���ȶ�����4��ţ�̵ı����614��593��379��242��203�� ����һ������722������700����ȥ
����һ������104��
����һ������887��887������700����ȥ��
����һ������088��
����һ������346
�ʴ�Ϊ��104��088��346��
�����������3�е�1������ʼ���Ҷ������ȶ�����4��ţ�̵ı����614��593��379��242����������λ��һ����������������ѡ���������ŵ���ȥ���������Ҷ�ȡ���ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������� ![]() �Ķ�����ΪA������g��x��=lg��x��1����x��[2��11]��ֵ��ΪB����A��BΪ��������
�Ķ�����ΪA������g��x��=lg��x��1����x��[2��11]��ֵ��ΪB����A��BΪ��������
A.�����ޣ�1��
B.�����ޣ�1]
C.[0��1]
D.��0��1]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=log2��x2��ax+1+a�������䣨���ޣ�2����Ϊ����������a��ȡֵ��ΧΪ�� ��
A.[4��+�ޣ�
B.[4��5]
C.��4��5��
D.[4��5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=1+2sinxcosx+2cos2x��
��1����f��x���������䣻
��2����f��x���ĶԳ��᷽�̣�
��3����f��x�������ֵ��д��ȡ���ֵʱ�Ա���x�ļ��ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() ʱ��������
ʱ��������![]() �ڵ�
�ڵ�![]() �������߷��̣�
�������߷��̣�
��2����![]() ��������㣬��
��������㣬��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�ķ��������Σ���Ϊ��������������Ρ�����������εĹ����ǣ������е�ÿһ�����������ں���һ�����������ڵ�������֮�ͣ������4�е�2���� ![]() ���ڵ�5���еĵ�2����
���ڵ�5���еĵ�2���� ![]() ���3����
���3���� ![]() ֮�ͣ�����
֮�ͣ�����
�ڡ�������������Ρ��У���10�д����ҵ�2��������8�����и����ĵ���֮��Ϊ�� ��
A.5010
B.5020
C.10120
D.10130
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ���ͼ�����ͼ�������ݸó����ͼ�ش��������⣺ 
��1���������x�ֱ�Ϊ2��4�������y��ֵ��
��2��˵���ó����ͼ�Ĺ��ܣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ü���������һ��ֱ������![]() ��һ��������
��һ��������![]() ��϶��ɣ�
��϶��ɣ� ![]() ��
�� ![]() ��
��

����֤����ƽ��![]() ƽ��
ƽ��![]() ��
��
������������![]() �ĸ�
�ĸ�![]() ��ʹ�ö����
��ʹ�ö����![]() ������ֵ��
������ֵ��![]() ��
��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com