
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD为菱形,∠ABC=60°,AA1![]() AB,M,N分别为AB,AA1的中点.
AB,M,N分别为AB,AA1的中点.
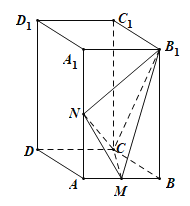
(1)求证:平面B1NC⊥平面CMN;
(2)若AB=2,求点N到平面B1MC的距离.
【答案】(1)见解析;(2)![]()
【解析】
(1)推导出AA1⊥平面ABCD,AA1⊥CM,CM⊥AB,从而CM⊥平面ABB1A1,进而CM⊥B1N,推导出△A1B1N∽△ANM,从而∠A1B1N=∠ANM,∠A1NB1=∠AMN,进而B1N⊥MN,B1N⊥平面CMN,由此能证明平面B1NC⊥平面CMN.
(2)求出点B1到平面CMN的距离为h1![]() ,设N到平面B1CM的距离为h2,由
,设N到平面B1CM的距离为h2,由![]() ,能求出点N到平面B1MC的距离.
,能求出点N到平面B1MC的距离.
(1)证明:∵直四棱柱ABCD﹣A1B1C1D1,∴AA1⊥平面ABCD,
∵CM平面ABCD,∴AA1⊥CM,
∵底面ABCD是菱形,∠ABC=60°,M是AB的中点,
∴CM⊥AB,
∵AA1∩AB=A,AA1平面ABB1A1,AB平面ABB1A1,
∴CM⊥平面ABB1A1,
∵B1N平面ABB1A1,∴CM⊥B1N,
∵M是AB中点,N为AA1中点,AA1![]() ,
,
∴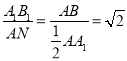 ,
,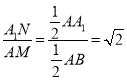 ,
,
∵∠B1A1N=∠NAM=90°,∴△A1B1N∽△ANM,
∴∠A1B1N=∠ANM,∠A1NB1=∠AMN,
∴∠A1NB1+∠ANM=90°,∴B1N⊥MN,
∵MN∩CM=M,∴B1N⊥平面CMN,
∵B1N平面B1NC,∴平面B1NC⊥平面CMN.
(2)∵在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD为菱形,∠ABC=60°,
AA1![]() AB,AB=2,M,N分别为AB,AA1的中点.
AB,AB=2,M,N分别为AB,AA1的中点.
∴MN![]() ,B1M
,B1M![]() 3,B1C
3,B1C![]() ,
,
B![]() ,
,
∵底面ABCD是菱形,∠ABC=60°,
∴CM![]() ,CN
,CN![]() ,
,
由(1)知B1N⊥平面CMN,设点B1到平面CMN的距离为h1,h1![]() ,
,
∵CN2=MN2+CM2,∴![]() ,
,
∴![]() ,
,
∵B1M=3,![]() ,∴
,∴![]() ,
,
设N到平面B1CM的距离为h2,
∵![]() ,
,
∴![]() ,
,
解得h2![]() .
.
∴点N到平面B1MC的距离为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,
为坐标原点,![]() 为坐标平面内动点,且
为坐标平面内动点,且![]() 成等差数列.
成等差数列.
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点
,过点![]() 作直线交
作直线交![]() 于
于![]() 两点(不与原点重合),是否存在
两点(不与原点重合),是否存在![]() 轴上一定点
轴上一定点![]() ,使得_________.若存在,求出定点
,使得_________.若存在,求出定点![]() ,若不存在,说明理由.从“①作
,若不存在,说明理由.从“①作![]() 点关于
点关于![]() 轴的对称点
轴的对称点![]() ,则
,则![]() 三点共线;②
三点共线;②![]() ”这两个条件中选一个,补充在上面的问题中并作答(注:如果选择两个条件分别作答,按第一个解答计分)
”这两个条件中选一个,补充在上面的问题中并作答(注:如果选择两个条件分别作答,按第一个解答计分)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥P﹣ABC中,平面PBC⊥平面ABC,∠ACB=90°,BC=PC=2,若AC=PB,则三棱锥P﹣ABC体积的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明和父母都喜爱《中国好声音》这栏节目,![]() 年
年![]() 月
月![]() 日晚在鸟巢进行中国好声音终极决赛,四强选手分别为李荣浩战队的邢晗铭,那英战队的斯丹曼簇,王力宏战队的李芷婷,庾澄庆战队的陈其楠,决赛后四位选手相应的名次为
日晚在鸟巢进行中国好声音终极决赛,四强选手分别为李荣浩战队的邢晗铭,那英战队的斯丹曼簇,王力宏战队的李芷婷,庾澄庆战队的陈其楠,决赛后四位选手相应的名次为![]() 、
、![]() 、
、![]() 、
、![]() ,某网站为提升娱乐性,邀请网友在比赛结束前对选手名次进行预测.现用
,某网站为提升娱乐性,邀请网友在比赛结束前对选手名次进行预测.现用![]() 、
、![]() 、
、![]() 、
、![]() 表示某网友对实际名次为
表示某网友对实际名次为![]() 、
、![]() 、
、![]() 、
、![]() 的四位选手名次做出的一种等可能的预测排列,
的四位选手名次做出的一种等可能的预测排列,![]() 是该网友预测的名次与真实名次的偏离程度的一种描述.
是该网友预测的名次与真实名次的偏离程度的一种描述.
(1)求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)按(1)中的结果,若小明家三人的排序号与真实名次的偏离程度都是![]() ,计算出现这种情况的概率(假定小明家每个人排序相互独立).
,计算出现这种情况的概率(假定小明家每个人排序相互独立).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.命题“若![]() ,则
,则![]() ”的否命题为:“若
”的否命题为:“若![]() ,则
,则![]() ”
”
B.命题“存在![]() ,使得
,使得![]() ”的否定是:“对任意
”的否定是:“对任意![]() ,均有
,均有![]() ”
”
C.命题“角![]() 的终边在第一象限角,则
的终边在第一象限角,则![]() 是锐角”的逆否命题为真命题
是锐角”的逆否命题为真命题
D.已知![]() 是
是![]() 上的可导函数,则“
上的可导函数,则“![]() ”是“
”是“![]() 是函数
是函数![]() 的极值点”的必要不充分条件
的极值点”的必要不充分条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是公差为1的等差数列,
是公差为1的等差数列,![]() 是单调递增的等比数列,且
是单调递增的等比数列,且![]() ,
,![]() ,
,![]() .
.
(1)求![]() 和
和![]() 的通项公式;
的通项公式;
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和
项和![]() ,求
,求![]() ;
;
(3)若数列![]() 的前
的前![]() 项积为
项积为![]() ,求
,求![]() .
.
(4)数列![]() 满足
满足![]() ,
,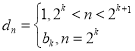 ,其中
,其中![]() ,
,![]() ,求
,求![]() .
.
(5)解决数列问题时,经常需要先研究陌生的通项公式,只有先把通项公式研究明白,然后尽可能转化为我们熟悉的数列问题,由此使问题得到解决.通过对上面(2)(3)(4)问题的解决,你认为研究陌生数列的通项问题有哪些常用方法,要求介绍两个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com