用数字1,2,3,4,5组成五位数,求其中恰有4个相同数字的概率.
【答案】
分析:本题考查的知识点是等可能事件的概率,我们先利用组合数公式,求出用数字1,2,3,4,5组成五位数的全部基本事件个数,再求出满足条件“恰有4个相同数字”的基本事件个数,然后代入古典概型公式,即可求出答案.
解答:解:五位数共有5
5个等可能的结果.
现在求五位数中恰有4个相同数字的结果数:
4个相同数字的取法有C
51种,另一个不同数字的取法有C
41种.
而这取出的五个数字共可排出C
51个不同的五位数,
故恰有4个相同数字的五位数的结果有C
51C
41C
51个,
所求概率P=
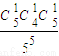
=
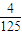
.
答:其中恰恰有4个相同数字的概率是
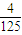
.
点评:古典概型要求所有结果出现的可能性都相等,强调所有结果中每一结果出现的概率都相同.弄清一次试验的意义以及每个基本事件的含义是解决问题的前提,正确把握各个事件的相互关系是解决问题的关键.解决问题的步骤是:计算满足条件的基本事件个数,及基本事件的总个数,然后代入古典概型计算公式进行求解.

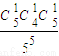 =
=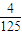 .
.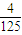 .
.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案