
【题目】已知数列{an}的前n项和Sn=﹣an﹣( ![]() )n﹣1+2(n∈N*),数列{bn}满足bn=2nan . (Ⅰ)求证数列{bn}是等差数列,并求数列{an}的通项公式;
)n﹣1+2(n∈N*),数列{bn}满足bn=2nan . (Ⅰ)求证数列{bn}是等差数列,并求数列{an}的通项公式;
(Ⅱ)设cn=log2 ![]() ,数列{
,数列{ ![]() }的前n项和为Tn , 求满足Tn
}的前n项和为Tn , 求满足Tn ![]() (n∈N*)的n的最大值.
(n∈N*)的n的最大值.
【答案】解:(Ⅰ)证明:∵Sn=﹣an﹣( ![]() )n﹣1+2(n∈N+),当n≥2时,Sn﹣1=﹣an﹣1﹣(
)n﹣1+2(n∈N+),当n≥2时,Sn﹣1=﹣an﹣1﹣( ![]() )n﹣2+2(n∈N+), ∴an=Sn﹣Sn﹣1=﹣an+an﹣1+(
)n﹣2+2(n∈N+), ∴an=Sn﹣Sn﹣1=﹣an+an﹣1+( ![]() )n﹣1 ,
)n﹣1 ,
化为2nan=2n﹣1an﹣1+1.
∵bn=2nan . ∴bn=bn﹣1+1,即当n≥2时,bn﹣bn﹣1=1.
令n=1,可得S1=﹣a1﹣1+2=a1 , 即a1= ![]() .
.
又b1=2a1=1,∴数列{bn}是首项和公差均为1的等差数列.
于是bn=1+(n﹣1)1=n=2nan ,
∴an= ![]() .
.
(Ⅱ)解:∵cn=log2![]() =n,
=n,
∴ ![]() =
= ![]() ﹣
﹣ ![]() ,
,
∴Tn=(1﹣ ![]() )+(
)+( ![]() ﹣
﹣ ![]() )+…(
)+…( ![]() ﹣
﹣ ![]() )=1+
)=1+ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() ,
,
由Tn![]() ,得1+
,得1+ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() ,即
,即 ![]() +
+ ![]() >
> ![]() ,
,
∵f(n)= ![]() +
+ ![]() 单调递减,f(4)=
单调递减,f(4)= ![]() ,f(5)=
,f(5)= ![]() ,
,
∴n的最大值为4
【解析】(Ⅰ)利用“当n≥2时,an=Sn﹣Sn﹣1”及其等差数列的通项公式即可得出.(Ⅱ)先求通项,再利用裂项法求和,进而解不等式,即可求得正整数n的最大值.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
【题目】将函数y=sinx的图象上所有点的横坐标缩短到原来的 ![]() 倍(纵坐标不变),再将所得的图象向左平移
倍(纵坐标不变),再将所得的图象向左平移 ![]() 个单位长度后得到函数f(x)的图象
个单位长度后得到函数f(x)的图象
(1)写出函数f(x)的解析式;
(2)若对任意的x∈[﹣ ![]() ,
, ![]() ],f2(x)﹣mf(x)﹣1≤0恒成立,求实数m的取值范围;
],f2(x)﹣mf(x)﹣1≤0恒成立,求实数m的取值范围;
(3)求实数a和正整数n,使得F(x)=f(x)﹣a在[0,nπ]上恰有2017个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平行六面体ABCD﹣A′B′C′D′,其中AB=4,AD=3,AA′=3,∠BAD=90°,∠BAA′=60°,∠DAA′=60°,则AC′的长为( ) 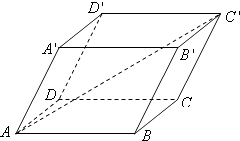
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1 , F2是椭圆与双曲线的公共焦点,P是它们的一个公共点,且|PF1|>|PF2|,椭圆的离心率为e1 , 双曲线的离心率为e2 , 若|PF2|=|F1F2|,则 ![]() +
+ ![]() 的最小值为( )
的最小值为( )
A.6+2 ![]()
B.8
C.6+2 ![]()
D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)为定义在R上的偶函数,当x≥0时,有f(x+3)=﹣f(x),且当x∈[0,3)时,f(x)=log4(x+1),给出下列命题:
①f(2015)>f(2014);
②函数f(x)在定义域上是周期为3的函数;
③直线x﹣3y=0与函数f(x)的图象有2个交点;
④函数f(x)的值域为[0,1).
其中不正确的命题个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某奶茶店为了解白天平均气温与某种饮料销量之间的关系进行分析研究,记录了2月21日至2月25日
的白天平均气温x(℃)与该奶茶店的这种饮料销量y(杯),得到如表数据:
平均气温x(℃) | 9 | 11 | 12 | 10 | 8 |
销量y(杯) | 23 | 26 | 30 | 25 | 21 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(2)试根据(1)求出的线性回归方程,预测平均气温约为20℃时该奶茶店的这种饮料销量.
(参考: ![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() ;9×23+11×26+12×30+10×25+8×21=1271,92+112+122+102+82=510)
;9×23+11×26+12×30+10×25+8×21=1271,92+112+122+102+82=510)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的方程为y2=10x,直线l的参数方程为 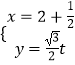 (t为参数),以坐标原点为极点,以x轴的正半轴为极轴建立极坐标系.
(t为参数),以坐标原点为极点,以x轴的正半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程和直线l的普通方程;
(2)设直线l与曲线C交于A、B两点,求弦长|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】偶函数f(x)满足f(1﹣x)=f(1+x),且在x∈[0,1]时,f(x)= ![]() ,若直线kx﹣y+k=0(k>0)与函数f(x)的图象有且仅有三个交点,则k的取值范围是 .
,若直线kx﹣y+k=0(k>0)与函数f(x)的图象有且仅有三个交点,则k的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“累计净化量(CCM)”是空气净化器质量的一个重要衡量指标,它是指空气净化器从开始使用到净化效率为![]() 时对颗粒物的累计净化量(单位:克).根据国家标准,对空气净化器的累计净化量(CCM)有如下等级划分:
时对颗粒物的累计净化量(单位:克).根据国家标准,对空气净化器的累计净化量(CCM)有如下等级划分:
累计净化量(克) |
|
|
| 12以上 |
等级 |
|
|
|
|
已知某批空气净化器共![]() 台,其累计净化量都分布在区间
台,其累计净化量都分布在区间![]() 内,为了解其质量,随机抽取了
内,为了解其质量,随机抽取了![]() 台净化器作为样本进行估计,按照
台净化器作为样本进行估计,按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 均匀分组,其中累计净化量在
均匀分组,其中累计净化量在![]() 的所有数据有:
的所有数据有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 和
和![]() ,并绘制了如下频率分布直方图.
,并绘制了如下频率分布直方图.
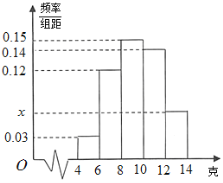
(1)求![]() 的值及频率分布直方图中
的值及频率分布直方图中![]() 的值;
的值;
(2)以样本估计总体,试估计这批空气净化器(共2000台)中等级为![]() 的空气净化器有多少台?
的空气净化器有多少台?
(3)从累计净化量在![]() 的样本中随机抽取2台,求恰好有1台等级为
的样本中随机抽取2台,求恰好有1台等级为![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com