
【题目】如图,在正四棱锥P﹣ABCD中,PA=AB=a,E是棱PC的中点. 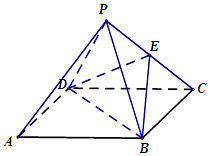
(1)求证:PC⊥BD;
(2)求直线BE与PA所成角的余弦值.
【答案】
(1)证明:∵四边形ABCD为正方形,且PA=AB=a,
∴△PBC,△PDC都是等边三角形,
∵E是棱PC的中点,
∴BE⊥PC,DE⊥PC,又 BE∩DE=E,
∴PC⊥平面BDE
又BD平面BDE,
∴PC⊥BD
(2)解:连接AC,交BD于点O,连OE.
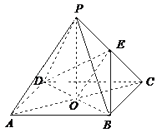
四边形ABCD为正方形,∴O是AC的中点
又E是PC的中点
∴OE为△ACP的中位线,∴AP∥OE
∴∠BOE即为BE与PA所成的角
在Rt△BOE中,BE= ![]() ,EO=
,EO= ![]() ,
,
∴ ![]() .
.
∴直线BE与PA所成角的余弦值为 ![]() .
.
【解析】(1)推导出△PBC,△PDC都是等边三角形,从而BE⊥PC,DE⊥PC,由此能证明PC⊥BD.(2)连接AC,交BD于点O,连OE,则AP∥OE,∠BOE即为BE与PA所成的角,由此能求出直线BE与PA所成角的余弦值.
【考点精析】掌握异面直线及其所成的角和直线与平面垂直的性质是解答本题的根本,需要知道异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系;垂直于同一个平面的两条直线平行.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,PA⊥平面ABC,AB⊥BC,DE垂直平分线段PC,且分别交AC,PC于D,E两点,PB=BC,PA=AB=1. 
(1)求证:PC⊥平面BDE;
(2)求直线BE与平面PAC所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位射击运动员,在某天训练中已各射击10次,每次命中的环数如下:
甲 7 8 7 9 5 4 9 10 7 4
乙 9 5 7 8 7 6 8 6 7 7
(Ⅰ)通过计算估计,甲、乙二人的射击成绩谁更稳;
(Ⅱ)若规定命中8环及以上环数为优秀,以频率作为概率,请依据上述数据估计,求甲在第11至
第13次射击中获得获得优秀的次数ξ的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图在棱锥P﹣ABCD中,ABCD为矩形,PD⊥面ABCD,PB=2,PB与面PCD成45°角,PB与面ABD成30°角. 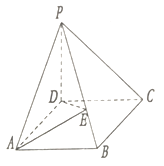
(1)在PB上是否存在一点E,使PC⊥面ADE,若存在确定E点位置,若不存在,请说明理由;
(2)当E为PB中点时,求二面角P﹣AE﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一直角墙角,两边的长度足够长,若P处有一棵树与两墙的距离分别是4m和am(0<a<12),不考虑树的粗细.现用16m长的篱笆,借助墙角围成一个矩形花圃ABCD.设此矩形花圃的最大面积为u,若将这棵树围在矩形花圃内,则函数u=f(a)(单位m2)的图象大致是( ) 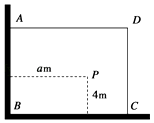
A.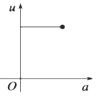
B.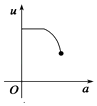
C.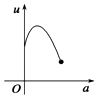
D.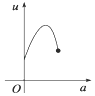
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知曲线 ![]() 及曲线
及曲线 ![]() ,C1上的点P1的横坐标为
,C1上的点P1的横坐标为 ![]() .从C1上的点
.从C1上的点 ![]() 作直线平行于x轴,交曲线C2于Qn点,再从C2上的点
作直线平行于x轴,交曲线C2于Qn点,再从C2上的点 ![]() 作直线平行于y轴,交曲线C1于Pn+1点,点Pn(n=1,2,3…)的横坐标构成数列{an}.
作直线平行于y轴,交曲线C1于Pn+1点,点Pn(n=1,2,3…)的横坐标构成数列{an}. 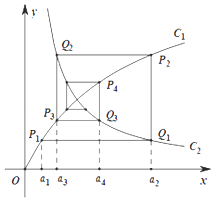
(1)求曲线C1和曲线C2的交点坐标;
(2)试求an+1与an之间的关系;
(3)证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆E: ![]() =1(a>b>0)的焦距为2,且过点(
=1(a>b>0)的焦距为2,且过点( ![]() ,
, ![]() ).
). 
(1)求椭圆E的方程;
(2)若点A,B分别是椭圆E的左、右顶点,直线l经过点B且垂直于x轴,点P是椭圆上异于A,B的任意一点,直线AP交l于点M. ①设直线OM的斜率为k1 , 直线BP的斜率为k2 , 求证:k1k2为定值;
②设过点M垂直于PB的直线为m.求证:直线m过定点,并求出定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com