
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() ,点
,点![]() ,过
,过![]() 的直线
的直线![]() 与圆
与圆![]() 交于点
交于点![]() ,过
,过![]() 做直线
做直线![]() 平行
平行![]() 交
交![]() 于点
于点![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过![]() 的直线与
的直线与![]() 交于
交于![]() 、
、![]() 两点,若线段
两点,若线段![]() 的中点为
的中点为![]() ,且
,且![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() .(2)
.(2)![]()
【解析】
(1)由题意可得![]() ,可得
,可得![]() ,则
,则![]() 的轨迹是焦点为
的轨迹是焦点为![]() ,
,![]() ,长轴为
,长轴为![]() 的椭圆的一部分,再用待定系数法即可求出方程;
的椭圆的一部分,再用待定系数法即可求出方程;
(2)由题意设直线方程为![]() ,设
,设![]() ,
,![]() ,联立直线与椭圆的方程,结合韦达定理表示出
,联立直线与椭圆的方程,结合韦达定理表示出![]() ,可得
,可得![]() ,设四边形
,设四边形![]() 的面积为
的面积为![]() ,则
,则![]() ,再根据基本不等式即可求出答案.
,再根据基本不等式即可求出答案.
解:(1)因为![]() ,又因为
,又因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以![]() 的轨迹是焦点为
的轨迹是焦点为![]() ,
,![]() ,长轴为
,长轴为![]() 的椭圆的一部分,
的椭圆的一部分,
设椭圆方程为![]() ,
,
则![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
所以椭圆方程为![]() ,
,
又因为点![]() 不在
不在![]() 轴上,所以
轴上,所以![]() ,
,
所以点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() ;
;
(2)因为直线![]() 斜率不为0,设为
斜率不为0,设为![]() ,
,
设![]() ,
,![]() ,联立
,联立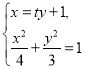 整理得
整理得![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
∵![]() ,∴
,∴![]() ,
,
设四边形![]() 的面积为
的面积为![]() ,
,
则![]()
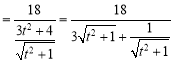 ,
,
令![]() ,
,
再令![]() ,则
,则![]() 在
在![]() 单调递增,
单调递增,
所以![]() 时,
时,![]() ,
,
此时![]() ,
,![]() 取得最小值
取得最小值![]() ,所以
,所以![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的上顶点为A,右焦点为F,O是坐标原点,
的上顶点为A,右焦点为F,O是坐标原点,![]() 是等腰直角三角形,且周长为
是等腰直角三角形,且周长为![]() .
.
(1)求椭圆的方程;
(2)若直线l与AF垂直,且交椭圆于B,C两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,短轴的两个端点分别为
,短轴的两个端点分别为![]() .
.
(Ⅰ)若![]() 为等边三角形,求椭圆
为等边三角形,求椭圆![]() 的方程;
的方程;
(Ⅱ)若椭圆![]() 的短轴长为
的短轴长为![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂有4台大型机器,在一个月中,一台机器至多出现1次故障,且每台机器是否出现故障是相互独立的,出现故障时需1名工人进行维修,每台机器出现故障需要维修的概率为![]() .
.
(1)问该厂至少有多少名维修工人才能保证每台机器在任何时刻同时出现故障时能及时进行维修的概率不小于![]() ?
?
(2)已知1名工人每月只有维修1台机器的能力,每月需支付给每位工人1万元的工资,每台机器不出现故障或出现故障能及时维修,能使该厂产生5万元的利润,否则将不产生利润.若该厂现有2名工人,求该厂每月获利的均值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com