
【题目】已知椭圆![]() :
:![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,左顶点为
,左顶点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过原点![]() 且与
且与![]() 轴不重合的直线交椭圆
轴不重合的直线交椭圆![]() 于
于![]() ,
,![]() 两点,直线
两点,直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
,![]() ,.求证:以
,.求证:以![]() 为直径的圆恒过交点
为直径的圆恒过交点![]() ,
,![]() ,并求出
,并求出![]() 面积的取值范围.
面积的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(Ⅰ)根据点![]() 在椭圆
在椭圆![]() 上,且△
上,且△![]() 的面积为
的面积为![]() ,结合性质
,结合性质![]() ,列出关于
,列出关于![]() 、
、![]() 、
、![]() 的方程组,求出
的方程组,求出![]() 、
、![]() 、
、![]() ,即可得椭圆
,即可得椭圆![]() 的方程;(Ⅱ)直线
的方程;(Ⅱ)直线![]() 的方程为
的方程为![]() ,设点
,设点![]() (不妨设
(不妨设![]() ),则点
),则点![]() ,由
,由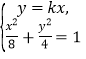 ,消去
,消去![]() 得
得![]() ,所以
,所以![]() ,
,![]() ,可证明
,可证明![]() ,
,![]() ,同理
,同理![]() ,则以img src="http://thumb.zyjl.cn/questionBank/Upload/2018/10/05/10/304d3c4b/SYS201810051001336893528698_DA/SYS201810051001336893528698_DA.024.png" width="29" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />为直径的圆恒过焦点
,则以img src="http://thumb.zyjl.cn/questionBank/Upload/2018/10/05/10/304d3c4b/SYS201810051001336893528698_DA/SYS201810051001336893528698_DA.024.png" width="29" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />为直径的圆恒过焦点![]() ,
,![]() ,可得
,可得![]() ,进而可得结果.
,进而可得结果.
试题解析:(Ⅰ)![]() ,
,![]() ,
,
又点![]() 在椭圆
在椭圆![]() 上,
上,![]() ,
,![]() ,
,
解得![]() ,或
,或![]() (舍去),又
(舍去),又![]() ,
,![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() ;
;
(Ⅱ)![]() ,
,![]() ,
,![]() ,
,
方法一:当直线![]() 的斜率不存在时,
的斜率不存在时,![]() ,
,![]() 为短轴的两个端点,则
为短轴的两个端点,则![]() ,
,![]() ,
, ![]() ,
,![]() ,则以
,则以![]() 为直径的圆恒过焦点
为直径的圆恒过焦点![]() ,
,![]() ,
,
当![]() 的斜率存在且不为零时,设直线
的斜率存在且不为零时,设直线![]() 的方程为
的方程为![]() ,
,
设点![]() (不妨设
(不妨设![]() ),则点
),则点![]() ,
,
由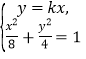 ,消去
,消去![]() 得
得![]() ,所以
,所以![]() ,
,![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,
,
因为直线![]() 与
与![]() 轴交于点
轴交于点![]() ,令
,令![]() 得
得![]() ,
,
即点![]() ,同理可得点
,同理可得点![]() ,
,
![]() ,
,![]() ,
,
![]() ,同理
,同理![]() ,
,
则以![]() 为直径的圆恒过焦点
为直径的圆恒过焦点![]() ,
,![]() ,
,
当![]() 的斜率存在且不为零时,
的斜率存在且不为零时,
![]() ,
,
![]() △
△![]() 面积为
面积为![]() ,
,
又当直线![]() 的斜率不存在时,
的斜率不存在时,![]() ,△
,△![]() 面积为
面积为![]() ,
,
![]() △
△![]() 面积的取值范围是
面积的取值范围是![]() .
.
方法二:当![]() ,
,![]() 不为短轴的两个端点时,设
不为短轴的两个端点时,设![]() ,
,
则![]() ,由点
,由点![]() 在椭圆
在椭圆![]() 上,
上, ![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,令
,令![]() 得
得![]() ,
,
即点![]() ,同理可得点
,同理可得点![]() ,
,
以![]() 为直径的圆可化为
为直径的圆可化为![]() ,
,
代入![]() ,化简得
,化简得![]() ,
,
令![]() 解得
解得![]()
![]() 以
以![]() 为直径的圆恒过焦点
为直径的圆恒过焦点![]() ,
,![]() ,
,
![]() ,又
,又![]() ,
,![]() ,
,
![]() △
△![]() 面积为
面积为![]() ,
,
当![]() ,
,![]() 为短轴的两个端点时,
为短轴的两个端点时,![]() ,△
,△![]() 面积为
面积为![]() ,
,
![]() △
△![]() 面积的取值范围是
面积的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】中欧班列是推进与“一带一路”沿线国家道路联通、贸易畅通的重要举措,作为中欧铁路在东北地区的始发站,沈阳某火车站正在不断建设.目前车站准备在某仓库外,利用其一侧原有墙体,建造一间墙高为3米,底面为12平方米,且背面靠墙的长方体形状的保管员室.由于此保管员室的后背靠墙,无需建造费用,因此甲工程队给出的报价为:屋子前面新建墙体的报价为每平方米400元,左右两面新建墙体报价为每平方米150元,屋顶和地面以及其他报价共计7200元.设屋子的左右两侧墙的长度均为![]() 米
米![]() .
.
(1)当左右两面墙的长度为多少时,甲工程队报价最低?
(2)现有乙工程队也参与此保管员室建造竞标,其给出的整体报价为![]() 元
元![]() ,若无论左右两面墙的长度为多少米,乙工程队都能竞标成功,试求
,若无论左右两面墙的长度为多少米,乙工程队都能竞标成功,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业有甲、乙两条生产线生产同种产品,现随机从这两条生产线上各抽取20件产品检测质量(单位:克),质量值落在![]() ,
, ![]() 的产品为三等品,质量值落在
的产品为三等品,质量值落在![]() ,
, ![]() 的产品为二等品,质量值落在
的产品为二等品,质量值落在![]() 的产品为一等品.下表为从两条生产线上各抽取的20件产品的质量检测情况,将频率视为概率,从甲生产线上随机抽取1件产品,为二等品的概率为0.2.
的产品为一等品.下表为从两条生产线上各抽取的20件产品的质量检测情况,将频率视为概率,从甲生产线上随机抽取1件产品,为二等品的概率为0.2.
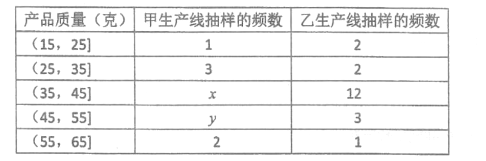
(1)求![]() 的值;
的值;
(2)现从两条生产线上的三等品中各抽取1件,求这两件产品的质量均在![]() 的概率;
的概率;
(3)估算甲生产线20个数据的中位数(保留3位有效数字).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 为梯形,
为梯形,![]() ,
,![]() ,且
,且![]() .
.

(Ⅰ)若点![]() 为
为![]() 上一点且
上一点且![]() ,证明:
,证明:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
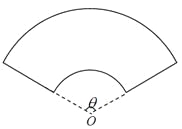
【题目】某单位拟建一个扇环面形状的花坛(如图所示),该扇环面是由以点![]() 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点![]() 的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为
的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为![]() 米,圆心角为
米,圆心角为![]() (弧度).
(弧度).
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)已知在花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 为何值时,
为何值时, ![]() 取得最大值?
取得最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 九章算术
九章算术![]() 是我国古代著名数学经典
是我国古代著名数学经典![]() 其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小
其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小![]() 以锯锯之,深一寸,锯道长一尺
以锯锯之,深一寸,锯道长一尺![]() 问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺
问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺![]() 问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示
问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示![]() 阴影部分为镶嵌在墙体内的部分
阴影部分为镶嵌在墙体内的部分![]() 已知弦
已知弦![]() 尺,弓形高
尺,弓形高![]() 寸,估算该木材镶嵌在墙中的体积约为( )(注:1丈
寸,估算该木材镶嵌在墙中的体积约为( )(注:1丈![]() 尺
尺![]() 寸,
寸,![]() ,
,![]() )
)

A. 600立方寸 B. 610立方寸 C. 620立方寸 D. 633立方寸
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com