练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    中，，将三角形绕斜边AC旋转一周所成的几何体的体积为      .

    解析试题分析：三角形绕斜边AC旋转一周所成的几何体是两个同底的圆锥，设底面半径是r，ABC的面积S=AB·BC= AC·r,所以，r=；所以几何体的体积V==.

    考点：圆锥体积.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    右图为某几何体的三视图，则该几何体的体积为

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    设甲、乙两个圆柱的底面积分别为，体积分别为，若它们的侧面积相等，且，则的值是        ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    已知球的直径SC=4，A.,B是该球球面上的两点，AB=2，∠ASC=∠BSC=45°，则棱锥S-ABC的体积为_________

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    圆锥的母线长为3，侧面展开图的中心角为，那么它的表面积为___________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    [2014·吉林质检]已知某组合体的正视图与侧视图相同，如图所示，其中AB＝AC，四边形BCDE为矩形，则该组合体的俯视图可以是________(把你认为正确的图的序号都填上)．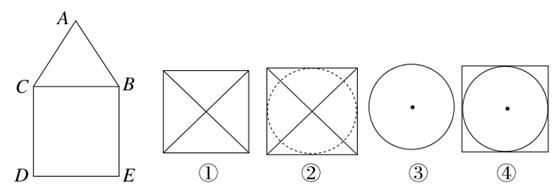

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    以长方体ABCD—A1B1C1D1的六条面对角线为棱，可以构成四面体A—B1CD1，A1—BC1D，若这两个四面体组合起来的体积为1（重合部分只算一次），则长方体的体积为
    （   ）

    A．2 B． C．3 D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    如图，体积为V的大球内有4个小球，每个小球的球面过大球球心且与大球球面有且只有一个交点，4个小球的球心是以大球球心为中心的正方形的4个顶点.V1为小球相交部分（图中阴影部分）的体积，V2为大球内、小球外的图中黑色部分的体积，则下列关系中正确的是

    A．V1= B． V2=
    C．V1> V2 D．V1< V2

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    下图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是(　　)

    A．9π B．10π C．11π D．12π

    查看答案和解析>>

    同步练习册答案