
【题目】已知函数f(x)=xlnx,函数g(x)=kx﹣cosx在点![]() 处的切线平行于x轴.
处的切线平行于x轴.
(1)求函数f(x)的极值;
(2)讨论函数F(x)=g(x)﹣f(x)的零点的个数.
【答案】(1)极小值为f(![]() )
)![]() ,无极大值(2)F(x)有且仅有2个零点
,无极大值(2)F(x)有且仅有2个零点
【解析】
(1)利用函数f(x)的导数判断函数的单调性,然后求出函数的极值;
(2)因为F(x)=x﹣cosx﹣xlnx,F'(x)=sinx﹣lnx,设h(x)=sinx﹣lnx,分类讨论:(i)当x∈(e,+∞)时,h(x)=F'(x)≤0,则F(x)单调递减,此时可得F(x)在(e,![]() )上存在唯一零点,也即在(e,+∞)上存在唯一零点;(ii)当x∈(
)上存在唯一零点,也即在(e,+∞)上存在唯一零点;(ii)当x∈(![]() ,e]时,
,e]时,![]() ,则F'(x)在(
,则F'(x)在(![]() ,e]单调递减,此时F(x)在(
,e]单调递减,此时F(x)在(![]() ,e]上恒大于0,无零点;(iii)当x∈(0,1)时,
,e]上恒大于0,无零点;(iii)当x∈(0,1)时,![]() ,所以
,所以![]() 在(0,1)上单调递减,此时F(x)在(
在(0,1)上单调递减,此时F(x)在(![]() ,
,![]() ]上存在唯一零点,即F(x)在(0,
]上存在唯一零点,即F(x)在(0,![]() ]上存在唯一零点
]上存在唯一零点
解:(1)因为函数f(x)=xlnx的定义域为(0,+∞),
所以![]() ,
,
令![]() ,即lnx+1<0,解得0<x
,即lnx+1<0,解得0<x![]() ,
,
所以f(x)的单调递减区间为(0,![]() ),
),
令![]() ,即lnx+1>0,解得
,即lnx+1>0,解得![]() ,
,
所以f(x)的单调递增区间为(![]() ,+∞),
,+∞),
综上,f(x)的极小值为f(![]() )
)![]() ,无极大值;
,无极大值;
(2)由![]() ,得
,得![]() )=k﹣1=0,故k=1,所以g(x)=x﹣cosx,
)=k﹣1=0,故k=1,所以g(x)=x﹣cosx,
因为F(x)=x﹣cosx﹣xlnx,![]() ,
,
设h(x)=sinx﹣lnx,
(i)当x∈(e,+∞)时,![]() ,则
,则![]() 单调递减,
单调递减,
又F(e)=﹣cose>0, ![]() ,
,
故F(x)在(e,![]() )上存在唯一零点,也即在(e,+∞)上存在唯一零点;
)上存在唯一零点,也即在(e,+∞)上存在唯一零点;
(ii)当x∈(![]() ,e]时,
,e]时, ![]() ,则
,则![]() 在
在![]() 单调递减,
单调递减,
因为![]() ,
,
所以存在![]() ,使得
,使得![]() ,且在
,且在![]() 上
上![]() ,在(x0,e]上
,在(x0,e]上![]() ,
,
所以![]() 为F(x)在(
为F(x)在(![]() ,e]上的最大值,
,e]上的最大值,
又因为F(e)=﹣cose>0,F(![]() )
)![]() (1﹣ln
(1﹣ln![]() )>0,
)>0,
所以F(x)在(![]() ,e]上恒大于0,无零点;
,e]上恒大于0,无零点;
(iii)当x∈(0,1)时,![]() ,
,
所以![]() 在(0,1)上单调递减,
在(0,1)上单调递减,
当x∈[1,![]() ]时,
]时,![]() ,
,
设t(x)=xcosx﹣1,所以![]() ,
,
所以t(x)在[1,![]() ]上单调递减,
]上单调递减,
所以t(x)<t(1)=cos1﹣1<0,即![]() ,
,
所以![]() 在(0,
在(0,![]() ]上单调递减,
]上单调递减,
因为![]() ,所以F(x)在
,所以F(x)在![]() 上单调递增,
上单调递增,
因为F(![]() )
)![]() (1﹣ln
(1﹣ln![]() )>0,
)>0,
![]() ,
,
所以F(x)在(![]() ,
,![]() ]上存在唯一零点,即F(x)在(0,
]上存在唯一零点,即F(x)在(0,![]() ]上存在唯一零点,
]上存在唯一零点,
综上,F(x)有且仅有2个零点


科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,
,![]() 分别为
分别为![]() 的中点,
的中点,![]() ,将
,将![]() 沿
沿![]() 折起,得到四棱锥
折起,得到四棱锥![]() ,
,![]() 为
为![]() 的中点.
的中点.
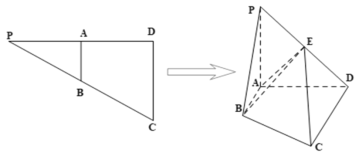
(1)证明:![]() 平面
平面![]() ;
;
(2)当正视图方向与向量![]() 的方向相同时,此时
的方向相同时,此时![]() 的正视图的面积为
的正视图的面积为![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ;数列
;数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
, ![]() ,
, ![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)是否存在正整数![]() ,使得
,使得![]() 恰为数列
恰为数列![]() 中的一项?若存在,求所有满足要求的
中的一项?若存在,求所有满足要求的![]() ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在我国瓷器的历史上六棱形的瓷器非常常见,因为六,八是中国人的吉利数字,所以好多器都做成六棱形和八棱形,数学李老师有一个正六棱柱形状的笔筒,底面边长为6cm,高为18cm(底部及筒壁厚度忽略不计),一长度为![]() cm的圆铁棒l(粗细忽略不计)斜放在笔筒内部,l的一端置于正六柱某一侧棱的展端,另一端置于和该侧棱正对的侧棱上.一位小朋友玩耍时,向笔筒内注水,恰好将圆铁棒淹没,又将一个圆球放在笔筒口,球面又恰好接触水面,则球的表面积为_____cm2.
cm的圆铁棒l(粗细忽略不计)斜放在笔筒内部,l的一端置于正六柱某一侧棱的展端,另一端置于和该侧棱正对的侧棱上.一位小朋友玩耍时,向笔筒内注水,恰好将圆铁棒淹没,又将一个圆球放在笔筒口,球面又恰好接触水面,则球的表面积为_____cm2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知点
中,已知点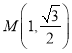 ,
,![]() 的参数方程为
的参数方程为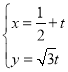 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】众所周知的“太极图”,其形状如对称的阴阳两鱼互抱在一起,也被称为“阴阳鱼太极图”.如图是放在平面直角坐标系中的“太极图”.整个图形是一个圆形.其中黑色阴影区域在y轴右侧部分的边界为一个半圆,给出以下命题:
①在太极图中随机取一点,此点取自黑色阴影部分的概率是![]()
②当![]() 时,直线y=ax+2a与白色部分有公共点;
时,直线y=ax+2a与白色部分有公共点;
③黑色阴影部分(包括黑白交界处)中一点(x,y),则x+y的最大值为2;
④设点P(﹣2,b),点Q在此太极图上,使得∠OPQ=45°,b的范围是[﹣2,2].
其中所有正确结论的序号是( )
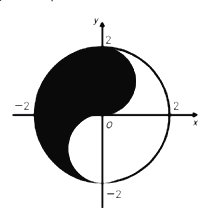
A.①④B.①③C.②④D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】受突如其来的新冠疫情的影响,全国各地学校都推迟2020年的春季开学.某学校“停课不停学”,利用云课平台提供免费线上课程.该学校为了解学生对线上课程的满意程度,随机抽取了500名学生对该线上课程评分.其频率分布直方图如下:若根据频率分布直方图得到的评分低于80分的概率估计值为0.45.
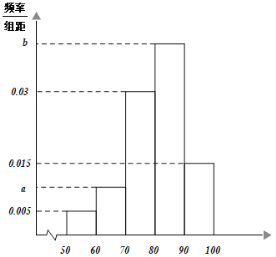
(1)(i)求直方图中的a,b值;
(ii)若评分的平均值和众数均不低于80分视为满意,判断该校学生对线上课程是否满意?并说明理由(同一组中的数据用该组区间的中点值为代表);
(2)若采用分层抽样的方法,从样本评分在[60,70)和[90,100]内的学生中共抽取5人进行测试来检验他们的网课学习效果,再从中选取2人进行跟踪分析,求这2人中至少一人评分在[60,70)内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com