
【题目】已知关于x的方程![]() ,
,![]()
(1)若方程有两个正根,求:m的取值范围;
(2)若方程有两个正根,且一个比2大,一个比2小,求m的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)方法一,一元二次方程有两个正根,两根之积、之和均取正值,用韦达定理表示,再加判别式大于等于0即可;方法二,构造函数,转化为二次函数的根的分布问题,要结合二次函数图象来解。由![]() 结合二次函数图象且方程有两个正根,可知函数图象开口向下,故只需满足
结合二次函数图象且方程有两个正根,可知函数图象开口向下,故只需满足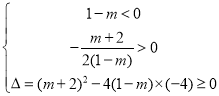 ,解不等式组即可;(2)构造函数
,解不等式组即可;(2)构造函数![]() ,由
,由![]() 结合二次函数图象且方程有两个正根,可知函数图象开口向下,由方程有两个正根,且一个比2大,一个比2小,可得
结合二次函数图象且方程有两个正根,可知函数图象开口向下,由方程有两个正根,且一个比2大,一个比2小,可得![]() ,解不等式组即可。
,解不等式组即可。
方法一,因为方程有两个正根,所以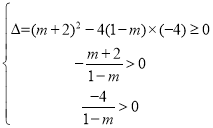 ,解得
,解得![]() 或
或![]() 。所以,m的取值范围为
。所以,m的取值范围为![]() 。
。
方法二,令 ![]() ,因为
,因为![]() ,方程有两个正根,所以函数
,方程有两个正根,所以函数![]() 的图象一定开口向下,所以
的图象一定开口向下,所以
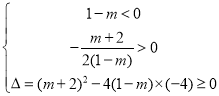 ,解得
,解得![]() 或
或![]() 。所以,m的取值范围为
。所以,m的取值范围为![]() 。
。
(2)令 ![]() ,因为
,因为![]() ,方程有两个正根,所以函数
,方程有两个正根,所以函数![]() 的图象一定开口向下,所以
的图象一定开口向下,所以
![]() ,解得
,解得![]() ,所以,m的取值范围为
,所以,m的取值范围为![]() 。
。


科目:高中数学 来源: 题型:
【题目】已知a,b,c分别为△ABC三个内角A,B,C的对边,2bcosA=acosC+ccosA.
(1)求角A的大小;
(2)若a=3,△ABC的周长为8,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前n项和为
的前n项和为![]() ,已知
,已知![]() ,
,![]() (
(![]() ).
).
(1)求证:数列![]() 为等比数列;
为等比数列;
(2)若数列![]() 满足:
满足:![]() ,
,![]() .
.
① 求数列![]() 的通项公式;
的通项公式;
② 是否存在正整数n,使得![]() 成立?若存在,求出所有n的值;若不存在,请说明理由.
成立?若存在,求出所有n的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司一年需购买某种原料400吨,设公司每次都购买![]() 吨,每次运费为4万元,一年的总存储费用为
吨,每次运费为4万元,一年的总存储费用为![]() 万元.
万元.
(1)要使一年的总运费与总存储费用之和最小,则每次购买多少吨?
(2)要使一年的总运费与总存储费用之和不超过200万元,则每次购买量在什么范围?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018河北保定市上学期期末调研】已知点![]() 到点
到点![]() 的距离比到
的距离比到![]() 轴的距离大1.
轴的距离大1.
(I)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(II)设直线![]() :
: ![]() ,交轨迹
,交轨迹![]() 于
于![]() 、
、![]() 两点,
两点, ![]() 为坐标原点,试在轨迹
为坐标原点,试在轨迹![]() 的
的![]() 部分上求一点
部分上求一点![]() ,使得
,使得![]() 的面积最大,并求其最大值.
的面积最大,并求其最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校社团活动开展有声有色,极大地推动了学生的全面发展,深受学生欢迎,每届高一新生都踊跃报名加入.现已知高一某班60名同学中有4名男同学和2名女同学参加心理社,在这6名同学中,2名同学初中毕业于同一所学校,其余4名同学初中毕业于其他4所不同的学校.现从这6名同学中随机选取2名同学代表社团参加校际交流(每名同学被选到的可能性相同).
(Ⅰ)在该班随机选取1名同学,求该同学参加心理社团的概率;
(Ⅱ)求从6名同学中选出的2名同学代表至少有1名女同学的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1且an﹣an﹣1=3×(![]() )n﹣2(n≥2,n∈N*).
)n﹣2(n≥2,n∈N*).
(1)求数列{an}的通项公式:
(2)若对任意的n∈N*,不等式1≤man≤5恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省高考改革方案指出:该省高考考生总成绩将由语文数学英语3门统一高考成绩和学生从思想政治、历史、地理、物理、化学、生物6门等级性考试科目中自主选择3个,按获得该次考试有效成绩的考生(缺考考生或未得分的考生除外)总人数的相应比例的基础上划分等级,位次由高到低分为A、B、C、D、E五等21级,该省的某市为了解本市![]() 万名学生的某次选考化学成绩水平,统计在全市范围内选考化学的原始成绩,发现其成绩服从正态分布
万名学生的某次选考化学成绩水平,统计在全市范围内选考化学的原始成绩,发现其成绩服从正态分布![]()
![]() ,现从某校随机抽取了
,现从某校随机抽取了![]() 名学生,将所得成绩整理后,绘制出如图所示的频率分布直方图.
名学生,将所得成绩整理后,绘制出如图所示的频率分布直方图.

(1)估算该校![]() 名学生成绩的平均值
名学生成绩的平均值![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)现从该校![]() 名考生成绩在
名考生成绩在![]() 的学生中随机抽取两人,该两人成绩排名(从高到低)在全市前
的学生中随机抽取两人,该两人成绩排名(从高到低)在全市前![]() 名的人数记为
名的人数记为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.参考数据:若
的分布列和数学期望.参考数据:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com