
分析 (1)由$\overrightarrow{PD}$=$\sqrt{3}$$\overrightarrow{MD}$得x0=x,y0=$\sqrt{3}$y,即可得到椭圆的方程及其离心率;
(2)由于已知坐标原点O到直线l的距离为$\frac{\sqrt{3}}{2}$,故求△AOB面积的最大值的问题转化为求线段AB的最大值的问题,由弦长公式将其表示出来,再判断最值即可得到线段AB的最大值.
解答 解:(Ⅰ)设M(x,y),P(x0,y0),由$\overrightarrow{PD}$=$\sqrt{3}$$\overrightarrow{MD}$得x0=x,y0=$\sqrt{3}$y …..(2分)
因为x02+y02=3,所以x2+3y2=3,即$\frac{{x}^{2}}{3}+{y}^{2}$=1,
其离心率e=$\frac{\sqrt{6}}{3}$.…..(4分)
(Ⅱ)当AB与x轴垂直时,|AB|=$\sqrt{3}$.(5分)
②当AB与x轴不垂直时,
设直线AB的方程为y=kx+m,A(x1,y1),B(x2,y2),
由已知$\frac{|m|}{\sqrt{1+{k}^{2}}}=\frac{\sqrt{3}}{2}$,得${m}^{2}=\frac{3}{4}({k}^{2}+1)$.(6分)
把y=kx+m代入椭圆方程,整理得(3k2+1)x2+6kmx+3m2-3=0,
∴x1+x2=$\frac{-6km}{3{k}^{2}+1}$,x1x2=$\frac{3({m}^{2}-1)}{3{k}^{2}+1}$(7分)
∴k≠0,|AB|2=(1+k2)(x2-x1)2=3+$\frac{12}{9{k}^{2}+\frac{1}{{k}^{2}}+6}$≤4,
当且仅当9k2=$\frac{1}{{k}^{2}}$,即k=$±\frac{\sqrt{3}}{3}$时等号成立,此时|AB|=2.(10分)
当k=0时,|AB|=$\sqrt{3}$.(11分)
综上所述:|AB|max=2,
此时△AOB面积取最大值$S=\frac{1}{2}|AB{|}_{max}×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$(12分)
点评 本题考查直线与圆锥曲线的综合问题,解答本题关键是对直线AB的位置关系进行讨论,可能的最值来,本题由于要联立方程求弦长,故运算量比较大,又都是符号运算,极易出错,做题时要严谨认真.利用弦长公式求弦长,规律固定,因此此类题难度降低不少,因为有此固定规律,方法易找,只是运算量较大.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$或$\sqrt{5}$ | B. | 2或5 | C. | $\sqrt{5}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
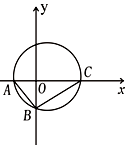 如图所示,在Rt△ABC中,已知A(-2,0),直角顶点$B(0,-2\sqrt{2})$,点C在x轴上.
如图所示,在Rt△ABC中,已知A(-2,0),直角顶点$B(0,-2\sqrt{2})$,点C在x轴上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com