【题目】已知函数
.
（Ⅰ）求函数
的单调区间；
（Ⅱ）若
恒成立，求实数
的取值范围.
【答案】（1）
的单调递减区间是
，单调递增区间是
.（2）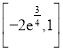
【解析】试题分析：（Ⅰ）函数求导
，定义域为
，由
，可得
或
进而讨论导函数的正负得函数单调性即可；
（Ⅱ）若
恒成立，只需
即可，讨论函数单调性求最值即可.
试题解析：
（Ⅰ）函数
的定义域为
，
.
由
，可得
或
，
当
时， 
在
上恒成立，
所以
的单调递增区间是
，没有单调递减区间；
当
时， 
的变化情况如下表：
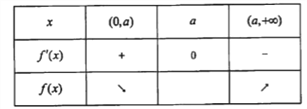
所以
的单调递减区间是
，单调递增区间是
.
当
时， 
的变化情况如下表：
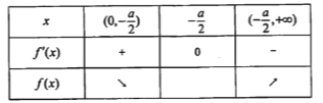
所以
的单调递减区间是
，单调递增区间是
.
（Ⅱ）由（Ⅰ）知，当
时， 
，符合题意.
当
时， 
的单调递减区间是
，单调递增区间是
，
所以
恒成立等价于
，即
，
所以
，所以
.
当
时， 
的单调递减区间是
，单调递增区间是
，
所以
恒成立等价于
，即
.
所以
，所以
.
综上所述，实数
的取值范围是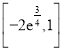
.
科目：高中数学 来源： 题型：
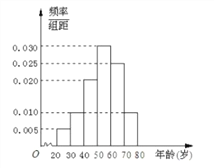
【题目】“中国人均读书4.3本（包括网络文学和教科书），比韩国的11本、法国的20本、日本的40本、犹太人的64本少得多，是世界上人均读书最少的国家.”这个论断被各种媒体反复引用，出现这样的统计结果无疑是令人尴尬的，而且和其他国家相比，我国国民的阅读量如此之低，也和我国是传统的文明古国、礼仪之邦的地位不相符.某小区为了提高小区内人员的读书兴趣，特举办读书活动，准备进一定量的书籍丰富小区图书站，由于不同年龄段需看不同类型的书籍，为了合理配备资源，现对小区内看书人员进行年龄调查，随机抽取了一天40名读书者进行调查，将他们的年龄分成6段： 
， 
， 
， 
， 
， 
后得到如图所示的频率分布直方图.问：
（1）估计在40名读书者中年龄分布在
的人数；
（2）求40名读书者年龄的平均数和中位数；
（3）若从年龄在
的读书者中任取2名，求这两名读书者年龄在
的人数
的分布列及数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知直线
的参数方程为
（
， 
为参数），曲线
的极坐标方程为
.
(1)将曲线
的极坐标方程化为直角坐标方程，并说明曲线
的形状；
(2)若直线
经过点
，求直线
被曲线
截得的线段的长.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设f(x)是定义域为R的周期函数，最小正周期为2，且
f(1＋x)＝f(1－x)，当－1≤x≤0时，f(x)＝－x.
(1)判断f(x)的奇偶性；
(2)试求出函数f(x)在区间[－1，2]上的表达式.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】定义在（0，+∞）上的单调函数f（x），x∈（0，+∞），f[f（x）﹣lnx]=1，则方程f（x）﹣f′（x）=1的解所在区间是 （ ）
A. （2，3） B. 
C. 
D. （1，2）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】函数
图象上不同两点
， 
处切线的斜率分别是
， 
，规定
（
为线段
的长度）叫做曲线
在点
与
之间的“弯曲度”，给出以下命题：
①函数
图象上两点
与
的横坐标分别为1和2，则
；
②存在这样的函数，图象上任意两点之间的“弯曲度”为常数；
③设点
， 
是抛物线
上不同的两点，则
；
④设曲线
（
是自然对数的底数）上不同两点
， 
，且
，若
恒成立，则实数
的取值范围是
．
其中真命题的序号为__________．（将所有真命题的序号都填上）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某城市随机抽取一年（365天）内100天的空气质量指数
（Air Pollution Index）的监测数据，结果统计如下：
|
|
|
|
|
|
| 大于300 |
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重 污染 | 重度污染 |
天数 | 10 | 15 | 20 | 30 | 7 | 6 | 12 |
（Ⅰ）若本次抽取的样本数据有30天是在供暖季，其中有7天为重度污染，完成下面
列联表，并判断能否有
的把握认为该市本年空气重度污染与供暖有关？
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 | 100 |
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 5.024 | 6.635 | 7.879 | 10.828 |
附：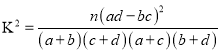 
（Ⅱ）政府要治理污染，决定对某些企业生产进行管控，当
在区间
时企业正常生产；当
在区间
时对企业限产
（即关闭
的产能），当
在区间
时对企业限产
，当
在300以上时对企业限产
，企业甲是被管控的企业之一，若企业甲正常生产一天可得利润2万元，若以频率当概率，不考虑其他因素：
①在这一年中随意抽取5天，求5天中企业被限产达到或超过
的恰为2天的概率；
②求企业甲这一年因限产减少的利润的期望值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
，其焦距为2，离心率为
（1）求椭圆
的方程；
（2）设椭圆的右焦点为
， 
为
轴上一点，满足
，过点
作斜率不为0的直线
交椭圆于
两点，求
面积
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
