
分析 等式左边各加数的函数名称都是正弦,角依次是第一个角的n倍,分析右边角的规律,即可得出结论.
解答 解:等式左边各加数的函数名称都是正弦,角依次是第一个角的n倍.
故左边通式应为sinx+sin2x+…+sinnx.
∵105°=$\frac{10°+200°}{2}$,100°=$\frac{200}{2}$;102°=$\frac{12°+192°}{2}$,96°=$\frac{192°}{2}$
故右边的通式应为$\frac{2sin\frac{1+n}{2}x•sin\frac{nx}{2}}{sinx}$
∴一般式为sinx+sin2x+…+sinnx=$\frac{2sin\frac{1+n}{2}x•sin\frac{nx}{2}}{sinx}$.
故答案为:sinx+sin2x+…+sinnx=$\frac{2sin\frac{1+n}{2}x•sin\frac{nx}{2}}{sinx}$(n∈N+).
点评 本题考查归纳推理,考查学生分析解决问题的能力,分析右边角的规律是关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
 已知x=$\frac{π}{6}$是函数f(x)=sin(2x+φ)(0<φ<$\frac{π}{2}$)图象的一条
已知x=$\frac{π}{6}$是函数f(x)=sin(2x+φ)(0<φ<$\frac{π}{2}$)图象的一条查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,5) | B. | (1,1) | C. | (3,1) | D. | (3,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
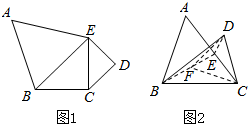 如图1,平面五边形ABCDE中,△ABE是边长为2的正三角形,△BCE、△CDE均为等腰直角三角形,且∠BCE和∠CDE为直角,现将△ABE、△CDE分别沿BE、CE折起,使平面ABE⊥平面BCE,平面DCE⊥平面BCE,如图2所示.
如图1,平面五边形ABCDE中,△ABE是边长为2的正三角形,△BCE、△CDE均为等腰直角三角形,且∠BCE和∠CDE为直角,现将△ABE、△CDE分别沿BE、CE折起,使平面ABE⊥平面BCE,平面DCE⊥平面BCE,如图2所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图△A′B′C′是△ABC的直观图,其中A′B′=A′C,那么△ABC是( )
如图△A′B′C′是△ABC的直观图,其中A′B′=A′C,那么△ABC是( )| A. | 等腰三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 钝角三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com