
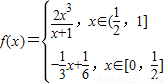 ,函数
,函数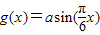 -2a+2(a>0),若存在x1、x2∈[0,1],使得f(x1)=g(x2)成立,则实数a的取值范围是 .
-2a+2(a>0),若存在x1、x2∈[0,1],使得f(x1)=g(x2)成立,则实数a的取值范围是 . 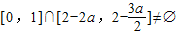 ,先看当二者的交集为空集时刻求得a的范围,进而可求得当集合的交集非空时a的范围.
,先看当二者的交集为空集时刻求得a的范围,进而可求得当集合的交集非空时a的范围.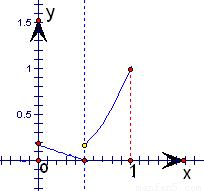 解:当x∈(
解:当x∈( ,1]时,
,1]时,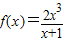 是增函数,y∈(
是增函数,y∈( ,1],
,1], ]时,f(x)=-
]时,f(x)=- x+
x+ 是减函数,
是减函数, ],如图.
],如图.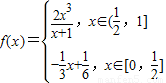 的值域为[0,1].
的值域为[0,1].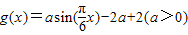 值域是
值域是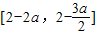 ,
, ,
,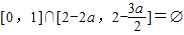 ,则2-2a>1或2-
,则2-2a>1或2-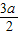 <0,即
<0,即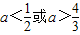 ,
,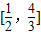 .
. .
.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源:2012-2013学年山西省长治二中高三(上)第一次练考数学试卷(理科)(解析版) 题型:填空题
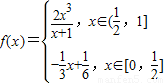 ,函数
,函数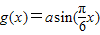 -2a+2(a>0),若存在x1、x2∈[0,1],使得f(x1)=g(x2)成立,则实数a的取值范围是 .
-2a+2(a>0),若存在x1、x2∈[0,1],使得f(x1)=g(x2)成立,则实数a的取值范围是 .查看答案和解析>>
科目:高中数学 来源:2012-2013学年黑龙江省哈尔滨九中高三(上)第二次月考数学试卷(理科)(解析版) 题型:填空题
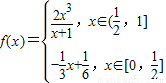 ,函数
,函数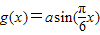 -2a+2(a>0),若存在x1、x2∈[0,1],使得f(x1)=g(x2)成立,则实数a的取值范围是 .
-2a+2(a>0),若存在x1、x2∈[0,1],使得f(x1)=g(x2)成立,则实数a的取值范围是 .查看答案和解析>>
科目:高中数学 来源:2012-2013学年黑龙江省哈尔滨九中高三(上)第二次月考数学试卷(文科)(解析版) 题型:填空题
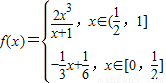 ,函数
,函数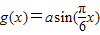 -2a+2(a>0),若存在x1、x2∈[0,1],使得f(x1)=g(x2)成立,则实数a的取值范围是 .
-2a+2(a>0),若存在x1、x2∈[0,1],使得f(x1)=g(x2)成立,则实数a的取值范围是 .查看答案和解析>>
科目:高中数学 来源:2012年全国高考数学领航试卷4(理科)(解析版) 题型:选择题
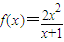 ,函数
,函数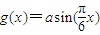 -2a+2(a>0),若存在x1、x2∈[0,1],使得f(x1)=g(x2)成立,则实数a的取值范围是( )
-2a+2(a>0),若存在x1、x2∈[0,1],使得f(x1)=g(x2)成立,则实数a的取值范围是( )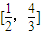
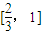

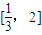
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com