
已知函数f(x)=(ax2+x)ex,其中e是自然数的底数,a∈R.
(1)当a<0时,解不等式f(x)>0;
(2)若f(x)在[-1,1]上是单调函数,求a的取值范围;
(3)当a=0时,求整数k的所有值,使方程f(x)=x+2在[k,k+1]上有解.
(1)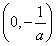 (2)
(2)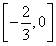 (3){-3,1}
(3){-3,1}
【解析】(1)因为ex>0,所以不等式f(x)>0即为ax2+x>0.
又a<0,所以不等式可化为x 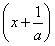 <0,所以不等式f(x)>0的解集为
<0,所以不等式f(x)>0的解集为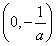 .
.
(2)f′(x)=(2ax+1)ex+(ax2+x)ex=[ax2+(2a+1)x+1]ex,
①当a=0时,f′(x)=(x+1)ex,f′(x)≥0在[-1,1]上恒成立,当且仅当x=-1时取等号,故a=0符合要求;
②当a≠0时,令g(x)=ax2+(2a+1)x+1,因为Δ=(2a+1)2-4a=4a2+1>0,所以g(x)=0有两个不相等的实数根x1、x2,不妨设x1>x2,因此f(x)有极大值又有极小值.若a>0,因为g(-1)·g(0)=-a<0,所以f(x)在(-1,1)内有极值点,故f(x)在[-1,1]上不单调.若a<0,可知x1>0>x2,因为g(x)的图象开口向下,要使f(x)在[-1,1]上单调,因为g(0)=1>0,必须满足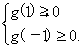 即
即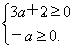 所以-
所以-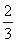 ≤a≤0.综上可知,a的取值范围是
≤a≤0.综上可知,a的取值范围是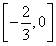 .
.
(3)当a=0时,方程即为xex=x+2,由于ex>0,所以x=0不是方程的解,所以原方程等价于ex-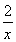 -1=0.
-1=0.
令h(x)=ex-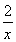 -1,因为h′(x)=ex+
-1,因为h′(x)=ex+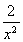 >0对于x∈(-∞,0)∪(0,+∞)恒成立,所以h(x)在(-∞,0)和(0,+∞)内是单调增函数,又h(1)=e-3<0,h(2)=e2-2>0,h(-3)=e-3-
>0对于x∈(-∞,0)∪(0,+∞)恒成立,所以h(x)在(-∞,0)和(0,+∞)内是单调增函数,又h(1)=e-3<0,h(2)=e2-2>0,h(-3)=e-3-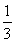 <0,h(-2)=e-2>0,所以方程f(x)=x+2有且只有两个实数根,且分别在区间[1,2]和[-3,-2]上,所以整数k的所有值为{-3,1}
<0,h(-2)=e-2>0,所以方程f(x)=x+2有且只有两个实数根,且分别在区间[1,2]和[-3,-2]上,所以整数k的所有值为{-3,1}


科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第14课时练习卷(解析版) 题型:解答题
已知函数f(x)=ax2-|x|+2a-1(a为实常数).
(1)若a=1,作函数f(x)的图象;
(2)设f(x)在区间[1,2]上的最小值为g(a),求g(a)的表达式;
(3)设h(x)=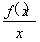 ,若函数h(x)在区间[1,2]上是增函数,求实数a的取值范围.
,若函数h(x)在区间[1,2]上是增函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第13课时练习卷(解析版) 题型:解答题
如图,两个工厂A、B相距2km,点O为AB的中点,要在以O为圆心,2km为半径的圆弧MN上的某一点P处建一幢办公楼,其中MA⊥AB,NB⊥AB.据测算此办公楼受工厂A的“噪音影响度”与距离AP的平方成反比,比例系数为1;办公楼受工厂B的“噪音影响度”与距离BP的平方也成反比,比例系数为4,办公楼与A、B两厂的“总噪音影响度”y是A、B两厂“噪音影响度”的和,设AP为xkm.

(1)求“总噪音影响度”y关于x的函数关系式,并求出该函数的定义域;
(2)当AP为多少时,“总噪音影响度”最小?
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第13课时练习卷(解析版) 题型:解答题
市场营销人员对过去几年某商品的价格及销售数量的关系作数据分析发现有如下规律:该商品的价格每上涨x%(x>0),销售数量就减少kx%(其中k为正常数).目前该商品定价为每个a元,统计其销售数量为b个.
(1)当k=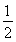 时,该商品的价格上涨多少,才能使销售的总金额达到最大?
时,该商品的价格上涨多少,才能使销售的总金额达到最大?
(2)在适当的涨价过程中,求使销售总金额不断增加时k的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第12课时练习卷(解析版) 题型:填空题
已知函数f(x)=lnx- (m∈R)在区间[1,e]上取得最小值4,则m=________.
(m∈R)在区间[1,e]上取得最小值4,则m=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第12课时练习卷(解析版) 题型:解答题
设函数f(x)=(x2+ax+b)ex(x∈R).
(1)若a=2,b=-2,求函数f(x)的极大值;
(2)若x=1是函数f(x)的一个极值点.
①试用a表示b;
②设a>0,函数g(x)=(a2+14)ex+4.若?ξ1、ξ2∈[0,4],使得|f(ξ1)-g(ξ2)|<1成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第三章第9课时练习卷(解析版) 题型:解答题
在△ABC中,角A,B,C的对边分别为a,b,c,C=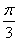 ,a=5,△ABC的面积为10
,a=5,△ABC的面积为10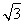
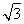 .
.
(1)求b,c的值;
(2)求cos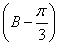 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com